missing data를 다루는 방법들

취업 후 현업에서 쓰이는 데이터를 직접 다뤄보니 Missing Data가 굉장히 많았습니다. Missing Data를 어떻게 핸들링 해야 좋을지에 대해 공부한 것을 정리해볼까 합니다.

1. 결측값이 생기는 이유

• Missing Data는 측정하고 저장한 데이터의 일부가 누락된 것을 의미한다.

• real world 에서 관측하는 대부분의 데이터는 Missing Data가 있다. 그럼 결측값이 생기는 이유는 뭘까?

  1. Missing Completely at Random (MCAR)

  • 정말 랜덤하게 누락된 케이스
  • 변수의 종류와 상관없이 전체적으로 비슷하게 누락된 데이터
  • 통계적으로 확인 가능한 missing pattern

  2. Missing at Random (MAR)

  • Missing Conditinally at Random 이라고도 함
  • 어떤 특정 변수에 관련하여 자료가 누락된 케이스
  • 결측값이 자료 내의 다른 변수와 관련되어 있는 경우 ex. 어떤 설문조사에서 일부 대상자가 설문지 바나대쪽 면이 있는 것을 모르고 채우지 않았을 경우

  3. Missing not at Random (MNAR)

  • 어떤 특정 변수에 관련하여 자료가 누락된 케이스
  • 결측값이 해당 변수와 연관이 있는 경우 ex. 어떤 설문조사에서 일부 질문에 정치적인 성향 등의 이유로 채우지 않았을 경우

MAR과 MCAR의 결측값은 제거하는 것이 좋다. 그러나 MNAR의 경우 결측값이 있는 데이터를 지운다면 모델이 편향될 가능성이 커지고, 일반화된 모델을 구하기 어려워진다. 따라서 결측값이 생기는 이유를 고려하여 데이터를 지울 것인지, 채울 것인지를 결정해야 한다.

참고로 Pandas에서 결측값은 None 또는 Nan으로 표현한다.

2. 해결 방법

1. Imputation : 누락된 데이터 대신 값을 채우는 방법
2. Deletion(Omission) : 분명하지 않은 결측값이 있는 데이터를 제거(생략)하는 방법

우선 Deletion에 대해 알아보도록 하자.

Deletioin : 살릴 수 없는 데이터는 버리자

Deletion에는 총 3가지 방법이 있다.

1. Listwise
2. Dropping
3. Pairwise

▶️ Listwise Deletioin : 결측값이 있다면 그 데이터는 버리자. 가장 쉬운 방법은 Missing Data가 있는 데이터를 지우는 방법이다. MNAR의 경우에는 모델이 편향될 가능성이 있으므로 주의해서 사용해야한다.

# df는 Pandasdml Dataframe 객체의 가상 이름
df.dropna() # 결측값이 있는 데이터 삭제
df.dropna(how='all') # 데이터의 모든 값이 Missing Value인 경우
df.drop(index, axis=0) # 배열 또는 단일 정수로 주어진 Index 모두 제거

▶️ Dropping Value : 특정 변수가 지나치게 비어있다면 변수를 과감하게 버리자 Listwise Deletion 과 유사한 방법으로 해당 변수(피처) 자체를 지우는 방법이 있다. 우리가 삭제하고자 하는 피처가 유용한 피처인지 모르기에 함부로 지워서는 안된다. 하지만 7 ~ 80%가 비어있는 변수라면 분석하기 어렵고, 이를 사용하기도 어렵기에 지우는 것이 나을 수도 있다.

df.dropna(axis='columns') # 결측값이 있는 피처 컬럼 모두 삭제
df.drop('column_name', axis=1)

✅ drop등 pandas에서 inplace=True라는 매개변수는 객체 자체를 변화시키는 코드이다. inplace=False를 사용하면 새로운 dataframe 객체를 생성하는 것이다.

▶️ Pairwise Deletion : 필요에 따라 사용하는 방법

필요한 경우에 따라서 데이터를 선별하는 것. A의 케이스에서는 [2,3] row를 사용하지 않고, B의 케이스에서는 [3,4] row를 사용하지 않는 등 원하는 방식으로 데이터를 사용하는 것이다. 여기서 누락하는 데이터를 MCAR이라고 가정한다.

Imputation : 인사이트와 통계로 데이터를 채우자

▶️ Mean, Median, Most_frequent: 대표값을 사용하자

from sklearn.impute import SimpleImputer

# 최빈값으로 Imputer 선언
imputer_mode = SimpleImputer(strategy='most_frequent')
imputer_mode.fit(categorical_data)

# 데이터 변환 (array로 반환하기 때문에 필요에 맞는 형태로 변환 후 사용)
categorical_data = imputer_mode.transform(categorical_data)

Mean : 평균을 이용한 대치

• 평균은 중심에 대한 경향성을 알 수 있는 척도
• 하지만 평균은 모든 관측치의 값을 모두 반영하므로 이상치의 영향을 많이 받기 때문에 주의해야함
• 평균을 이용하기 때문에 수치형 변수에만 적용 가능

Median : 중간값을 이용한 대치

• 데이터의 정중앙에 위치한 관측값을 의미함
• 모든 관측치의 값을 반영하지 않으므로 이상치의 영향을 덜 받음
• 중간값을 이용한 이 방식 또한 수치형 변수에만 사용 가능

Most_frequent : 최빈값

• 범주 내에서 가장 자주 등장한 관측값
• 빈도수를 사용하기 때문에 범주형 변수에만 사용 가능

MICE : 자동 대치

from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer

# random_state값은 원하시는 숫자 아무거나 넣으시면 됩니다.
imputer_mice = IterativeImputer(random_state=83)
numeric_data = imputer_mice.fit_transform(numeric_data)

• Round robin 방식을 반복하여 결측 값을 회귀하는 방식으로 결측치를 처리
• Multivariate Imputation By Chained Equations 알고리즘의 약자로, 다른 열의 데이터를 보고 누락된 값에 대한 최적의 예측치를 추정하여 누락된 값을 손쉽게 대치 할 수 있는 기술이다.
• 결측 값을 회귀하는 방식으로 처리하기 때문에 수치형 변수에 해당
• 범주형 변수에 사용하려면 인코딩을 해야함

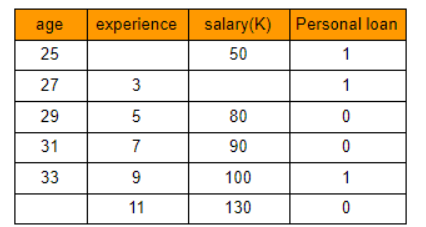
예를 들어, 개인 대출 홍보를 위해 데이터 샘플을 기록한다고 하자.

이제 표에서 누락된 값을 채워야한다

정답값은 위와 같다. 이제 빈칸을 어떻게 채우는지 알아보자.

우선 Person loan은 조사 목적이므로 제외하자.

그렇게하면 위와 같은 표가 나온다.

여기서 Mean, Medium과 같은 평균 대치 방법을 사용하지 않는 이유는 Mean, Medium과 같은 방법은 특정 열을 사용하여 해당 열의 결측치를 대치하기 때문이다.

평균 대치를 사용하면 위와 같은 결과가 나오게 된다.

25살이 경력이 7년이고 27살에 90K의 돈을 받는다는 것은 말이 되지 않는다.

따라서 MICE 방법을 사용해야 한다. MICE 방법은 결측값을 보다 더 잘 예측하기 위해 데이터의 다른 변수를 고려한다. 알고리즘 수행 순서는 다음과 같다.

1. 각 열의 평균으로 평균 대치를 사용하여 모든 결측치를 대치한다. 이것을 제로 데이터셋 이라고 한다.

1. 나머지 특성과 행(experience, salary의 상위 5개 행)은 특성 매트릭스(보라색 셀)이 되고, age가 구하고자 하는 변수(노란색 셀)이 된다. X=experience 및 salary, Y=age로 채워진 행에 대해 선형 회귀 모델을 실행한다. 결측 연령을 추정하기 위해 결측치가 속한 행(흰색 셀)을 테스트 데이터로 사용한다.

1. 이렇게 하면, 상위 5개 행은 학습 데이터가 되고 age가 누락된 행은 테스트 데이터가 된다. 이제 age=11, salary=130을 사용하여 해당 age를 예측한다.

선형 회귀 모델을 실행했을 때, 34.99로 예측한 것을 확인할 수 있다.

1. age열의 누락된 셀에서 예상 age 값을 업데이트한다. 이제 expreience에 부여된 값을 제거한다. 위와 같은 방식으로 선형 회귀 모델을 실행하면 0.98이 나온다.

1. 마지막으로 experience를 업데이트하고 salary를 지운다. 앞서 했던 것과 같은 방식으로 예측을 수행하면 70이 된다.

이제 원래 데이터셋의 누락된 값을 대치했고 첫 번째 반복 실행 후 예측된 값이 표시된다.

1. 0 번째와 첫 번째 데이터 세트를 뺀다. 결과 데이터셋은 다음과 같다.

1. 이제 첫 번째 데이터셋을 기본 데이터셋으로 대치하고 means 대치가 있는 제로 데이터셋을 버린다.

최종적으로 다음과 같은 결과를 얻게 된다.

이런 식으로 반복 작업을 수행해서 차이를 0에 가깝게 만들면 된다.

이런 대표값을 사용하는 방법은 매우 빠르지만, 단점 또한 많다.

1. 다른 피처 간의 상관도를 전혀 고려하지 않는다
2. 비슷한 느낌으로 경향성에 대한 고려가 없다
3. 정확도가 떨어진다
4. 평균의 경우, 분산이 줄어든다
5. 최빈값의 경우, 데이터 전체에 편향이 생긴다.

from sklearn.impute import SimpleImputer
imp_mean = SimpleImputer( strategy='most_frequent') # mean, median
imp_mean.fit(train)
imputed_train_df = imp_mean.transform(train)

▶️ Multiple Imputation(MI) : 좋은 거 + 좋은 거 = 좋은 거

Imputation으로 인한 노이즈 증가 문제를 해결하기 위한 방법이다. 단순하게 한 번 Imputation을 진행한 것보다 여러 Imputation을 조합하는 것이 더 좋다는 아이디어이다. 모든 MI는 3가지 과정을 거친다.

1. Imputation : distribution을 토대로 m개의 데이터셋을 imputation 합니다. 이 과정에서 Markov Chain Monte Carlo (MCMC)를 사용하면 더 나은 결과를 얻을 수 있다고 한다
2. Analysis : m개의 완성된 데이터셋을 분석한다
3. Pooling : 평균, 분산, 신뢰 구각을 계산하여 결과를 합친다

MI도 여러가지 방법이 있지만, 그 중에서 가장 우선되는 방법이 multiple imputation by chained equations(MICE) 이다. 다른 방법으론, fully conditional specification 과 sequential regression multiple imputation 이 있다.

▶️ KNN(K-Nearest Neighbors) : ML을 위한 ML

ML의 기본적인 알고리즘 중 하나인 KNN을 사용하는 방법도 있다. KNN은 본인과 가까운 k개의 데이터를 선택하여, 그 평균을 취하는 방식이다.

mean, mode 등에 비해 정확하다는 단점이 있지만, KNN이 가지는 단점을 그대로 가져온다.

1. 계산량이 많다
2. outlier에 민감하다
3. feature의 scale이 중요하다(유클리드 or 맨하튼 거리를 기반으로 하기 때문에)
4. 고차원 데이터에서 매우 부정확하다

from fancyimpute import KNN
knnOutput = KNN(k=5).complete(mydata) # k값으로 이웃값 조정

▶️ 좋은 알고리즘을 사용하자

Boost 계열의 알고리즘은 이런 결측값이 있어도 잘 예측한다.

• XGBoost
• LightGBM
• CatBoost

3. 결론

지금 회사에서 하고 있는 프로젝트에선 결측률을 낮추기 위해 MICE 방법을 사용하고 있다. 문제는 이 방식을 사용해도 머신러닝 모델의 성능이 눈에 띄게 좋아지지는 않는다는 것이다. 0.47 --> 0.51 이 되었다 😢. 결측률을 낮추는 좋은 방법은 내가 공부한 방법 말고도 많을 것이다. 시간이 날때마다 틈틈히 공부해 봐야겠다.

4. 참조

---

• Hello Subinium!

• ICHI.PRO