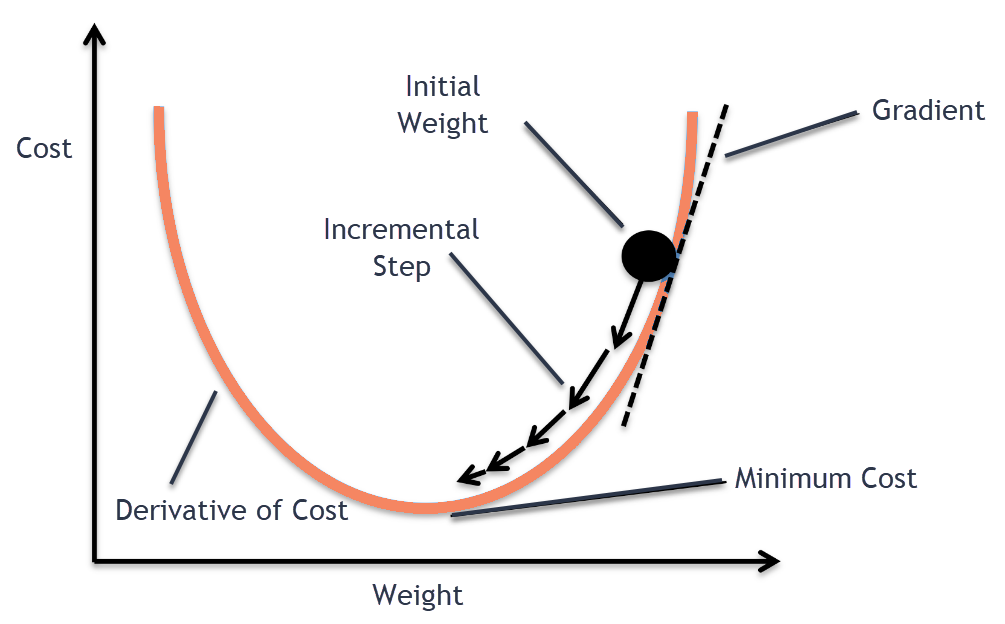
gradient descent 직접 구현해보기

gradient descent 방법은 1차 미분계수를 이용해 함수의 최소값을 찾아가는 iterative한 방법입니다. 비용 함수(Cost function 혹은 loss function)를 최소화 하기 위해 반복해서 파라미터를 업데이트하는 방식입니다. 그 과정을 PyTorch와 matplotlib을 이용해서 시각화 해보도록 하겠습니다.

1. 필요한 모듈 import 해오기

# 모듈 import 
from IPython.display import Image
import matplotlib.pyplot as plt
import numpy as np
import torch

2. 샘플 데이터셋 생성

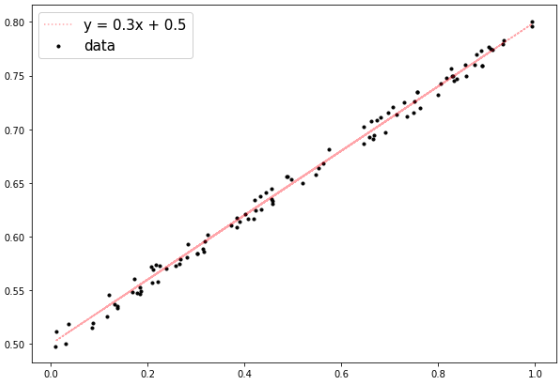
• y = 0.3x + 0.5의 선형회귀 식을 추종하는 샘플 데이터셋을 생성합니다.
• 경사하강법 알고리즘으로 w=0.3, b=0.5를 추종하는 결과를 도출해 볼 것 입니다.

def make_linear(w=0.5, b=0.8, size=50, noise=1.0):
    x = np.random.rand(size) # x 좌표
    y = w * x + b # y 좌표
    noise = np.random.uniform(-abs(noise), abs(noise), size=y.shape) # 데이터에 불규칙한 변동을 추가하여 실제 세계의 데이터를 모델링할 때 발생하는 불확실성을 반영
    yy = y + noise # y에 noise를 더한 값으로 계산. 즉, 실제 데이터에 잡음을 추가한 결과
    plt.figure(figsize=(10, 7))
    plt.plot(x, y, color='r', label=f'y = {w}x + {b}', linestyle=':', alpha=0.3)
    plt.scatter(x, yy, color='black', label='data', marker='.')
    plt.legend(fontsize=15)
    plt.show()
    print(f'w: {w}, b: {b}')
    return x, yy

x, y = make_linear(w=0.3, b=0.5, size=100, noise=0.01)

3. 샘플 데이터셋인 x와 y를 torch.as_tensor()로 텐서(Tensor) 변환하기

x = torch.as_tensor(x)
y = torch.as_tensor(y)

4. 랜덤한 w, b를 생성하기

• torch.rand(1)은 torch.Size[1]`을 가지는 normal 분포의 랜덤 텐서를 생성한다.

# random 한 값으로 w, b를 초기화 합니다.
w = torch.rand(1)
b = torch.rand(1)

print(w.shape, b.shape)

# requires_grad = True로 설정된 텐서에 대해서만 미분을 계산합니다.
w.requires_grad = True
b.requires_grad = True

5. 가설함수(Hypothesis Function)을 생성하기

y_hat = w * x + b

6. y_hat과 y의 손실(Loss)를 계산한다. 손실함수는 MSE를 사용한다.

# 손실함수 정의
loss = ((y_hat - y) ** 2).mean()

7. loss.backward() 호출 시 미분 가능한 텐서에 대해 미분을 계산한다.

# 미분 계산(back propagation)
loss.backward()

• w와 b의 미분 값을 확인해보자

w.grad, b.grad

# (tensor([0.0106]), tensor([-0.0729]))

8. graient descent 구현

• 최대 500번의 iteration(epoch)동안 반복하여 w,b의 미분을 업데이트하면서, 최소의 손실(loss)에 도달하는 w, b를 산출한다

• learning_rate는 임의의 값으로 초기화 하였으며, 0.1로 설정한다.

• 하이퍼 파라미터(hyper-parameter) 정의

# 최대 반복 횟수 정의
num_epoch = 500

# 학습율(learning_rate)
learning_rate = 0.1

# loss, w, b를 기록하기 위한 list 정의
losses = []
ws = []
bs = []

# random한 값으로 w,b를 초기화
w = torch.rand(1)
b = torch.rand(1)

# 미분 값을 구하기 위하여 requires_grad는 True로 설정
w.requires_grad = True
b.requires_grad = True

for epoch in range(num_epoch):
    
    # Affine Function
    y_hat = x * w + b

    # 손실(loss) 계산
    loss = ((y_hat - y)**2).mean()

    # 손실이 0.00005 보다 작으면 break
    if loss < 0.00005:
        break

    # w, b의 미분 값인 grad 확인 시 다음 미분 계산 값은 None이 return됨
    # 이러한 현상을 방지하기 위하여 retain_grad()를 loss.backward() 이전에 호출함
    w.retain_grad()
    b.retain_grad()

    # 미분 계산
    loss.backward()

    # 경사하강법 계산 및 적용
    # w에 learning_rate * (gradient w)를 차감함
    w = w - learning_rate * w.grad

    # b에 learning_rate * (gradient b)를 차감함
    b = b - learning_rate * b.grad

    # 계산된 loss, w, b를 저장함
    losses.append(loss.item())
    ws.append(w.item())
    bs.append(b.item())

    if epoch % 5 == 0:
        print("{0:03d} w = {1:.5f}, b = {2:.5f} loss = {3:.5f}".format(epoch, w.item(), b.item(), loss.item()))
    
print("----" * 15)
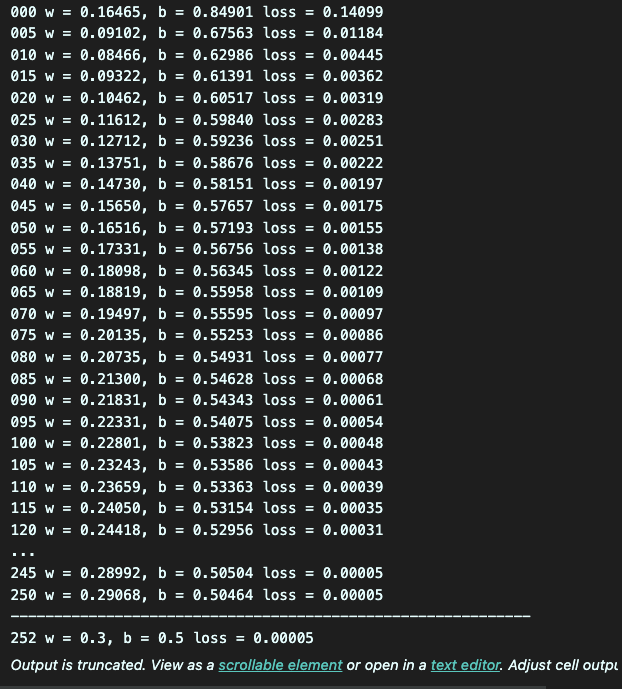
print("{0:03d} w = {1:.1f}, b = {2:.1f} loss = {3:.5f}".format(epoch, w.item(), b.item(), loss.item()))

랜덤으로 w 와 b를 생성했을 땐 각각 0.16465, 0.84901 로 loss값 0.14099를 기록하면서 정답값인 w = 0.3, b = 0.5와 큰 차이를 보였지만, iteration이 반복될 수록 그 값이 점차 줄어나가는 것을 확인할 수 있다.

9. 결과 시각화

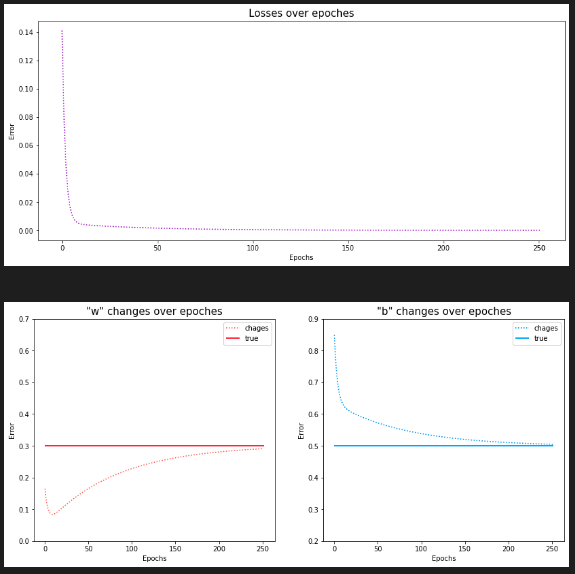
• loss는 epoch이 늘어남에 따라 감소함

• epoch 초기에는 급격히 감소하다가, 점차 완만하게 감소함을 확인할 수 있는데 이는 초기에는 큰 미분값이 업데이트 되지만, 점차 계산된 미분 값이 작아지게 되고 결국 업데이트가 작게 일어나면서 손실은 완만하게 감소한다.

• w, b도 초기값은 0.3, 0.5와 다소 먼 값이 설정되었지만, 점차 정답을 찾아가게 된다

# 전체 loss 에 대한 변화량 시각화
plt.figure(figsize=(14, 6))
plt.plot(losses, c='darkviolet', linestyle=':')

plt.title('Losses over epoches', fontsize=15)
plt.xlabel('Epochs')
plt.ylabel('Error')
plt.show()

# w, b에 대한 변화량 시각화
fig, axes = plt.subplots(1, 2)
fig.set_size_inches(14, 6)

axes[0].plot(ws, c='tomato', linestyle=':', label='chages')
axes[0].hlines(y=0.3, xmin=0, xmax=len(ws), color='r', label='true')
axes[0].set_ylim(0, 0.7)
axes[0].set_title('"w" changes over epoches', fontsize=15)
axes[0].set_xlabel('Epochs')
axes[0].set_ylabel('Error')
axes[0].legend()

axes[1].plot(bs, c='dodgerblue', linestyle=':', label='chages')
axes[1].hlines(y=0.5, xmin=0, xmax=len(ws), color='dodgerblue', label='true')
axes[1].set_ylim(0.2, 0.9)
axes[1].set_title('"b" changes over epoches', fontsize=15)
axes[1].set_xlabel('Epochs')
axes[1].set_ylabel('Error')
axes[1].legend()

plt.show()

결론

가중치와 편향이 점차 수렴해나가는 gradient descent를 시각화 해보았다. 머리 속으로만 그려지던게 시각화가 되니 직관적으로 이해하는 것에 도움이 되는 것 같다.

참조

---

• 테디노트