RNN

RNN에 대해 알아보자.

순환 신경망(Recurrent Neural Network, RNN)

0. RNN? 그런데 FNN(Feed Forward Neural Network)을 곁들인

시계열 데이터의 경우 이전의 정보가 다음의 결과에 영향을 미치기 때문에 FNN만으로는 충분하지 않다. 따라서 시간에 따라 누적된 정보를 처리할 수 있는 신경망 인 RNN이 등장하게 되었다.

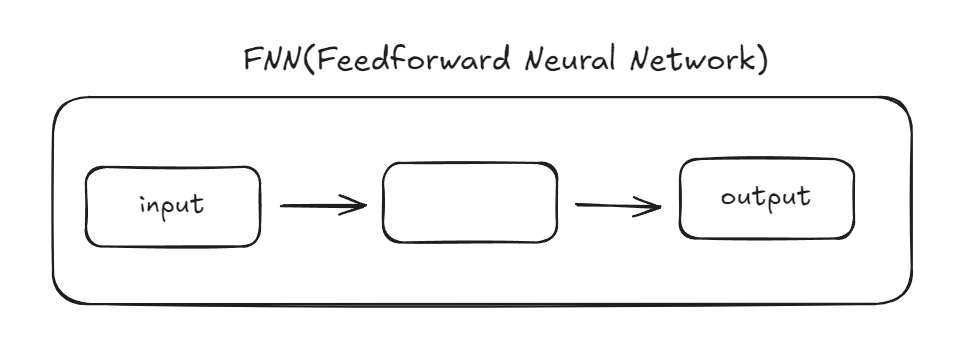
FNN은 입력이 출력층으로 향하는 구조를 갖는다. 각 층에서 가중치와 편향을 곱하고 활성화 함수를 통해 입력값을 변환한다. 출력은 각 층의 결과의 계산에 기반한다.

RNN은 시간에 따라 누적된 정보를 처리할 수 있는 신경망이다. RNN은 메모리 셀을 갖고 있기 때문에 시간에 따라 정보를 저장하고, 이전의 정보를 이용하여 현재의 결과를 예측하거나 분류 할 수 있다.

1. 순환 신경망(Recurrent Neural Network, RNN)

---

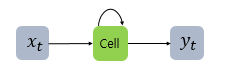
RNN은 은닉층의 노드에서 활성화 함수를 통해 나온 결과값을 출력층 방향으로도 보내면서, 다시 은닉층 노드의 다음 계산의 입력으로 보내는 특징을 갖는다.

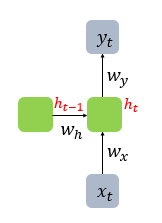
x는 입력층의 입력 벡터, y는 출력층의 출력 벡터이다.. RNN에서는 은닉층에서 활성화 함수를 통해 결과를 내보내는 역할을 하는 노드를 셀(cell)이라고 표현한다. 이 셀은 이전의 값을 기억하려고 하는 일종의 메모리 역할을 수행하므로 이를 메모리 셀 또는 RNN 셀 이라고 표현한다.

은닉층의 메모리 셀은 각각의 시점(time stamp)에서 바로 이전 시점에서의 은닉층의 메모리 셀에서 나온 값을 자신의 입력으로 사용하는 재귀적 활동을 하고 있다. 현재 시점 t에서의 메모리 셀이 갖고 있는 값은 과거의 메모리 셀들의 영향을 받은 것이다. 이 때, 메모리 셀이 출력층 방향 또는 다음 시점인 $t+1$의 자신에게 보내는 값을 은닉 상태(hidden state) 라고 한다. 즉, t 시점의 메모리 셀은 $t-1$ 시점의 메모리 셀이 보낸 은닉 상태값을 t 시점의 은닉 상태 계산을 위한 입력값으로 사용하게 되는 것이다.

피드 포워드 신경망에서는 뉴런이라는 단위를 사용했지만, RNN에서는 입력층과 출력층에서는 각각 입력 벡터와 출력 벡터, 은닉층에서는 은닉 상태라고 한다.

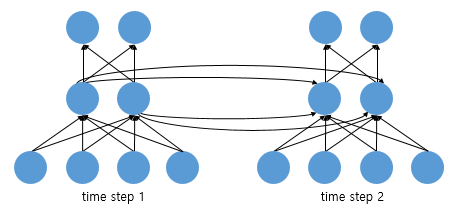
위 그림을 예로 들면, 입력 벡터의 차원이 4, 은닉 상태의 크기가 2, 출력층의 출력 벡터의 차원이 2인 RNN이 시점이 2일 때의 모습을 보여준다고 할 수 있다.

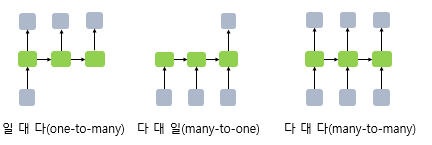
RNN은 입력과 출력의 길이를 다르게 설계하여 다양한 용도로 사용할 수 있다. RNN 셀의 각 시점의 입, 출력의 단위는 사용자가 정의하기 나름이지만 가장 보푠적인 단위는 ‘단어 벡터’ 이다.

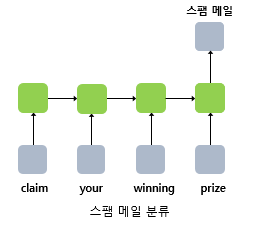
예를 들어, 단어 시퀀스에 대해서 하나의 출력을 하는 다 대 일(many-to-one) 구조의 모델은 입력 문서가 긍정적인지 부정적인지를 판별하는 감성 분류, 스펨 메일 분류 등에 사용할 수 있다.

RNN에 대한 수식을 정의하면 다음과 같다.

• $h_t$ : 현재 시점 t에서의 은닉 상태값
• $W_x$ : 입력층을 위한 가중치
• $W_h$ : 이전 시점 t-1의 은닉 상태값인 $h_{t-1}$을 위한 가중치

위 정의를 바탕으로 식으로 표현하면 다음과 같다.

• 은닉층 : $h_t = thanh({W_x}x_t + {W_h}h_{t-1} + b)$
• 출력층 : $y_t = f({W_y}h_t + b)$

단, f는 비선형 활성화 함수 중 하나.

2. 케라스(Keras)로 RNN 구현하기

---

• hidden_units : 은닉 상태의 크기를 정의. 메모리 셀이 다음 시점의 메모리 셀과 출력층으로 보내는 값의 크기(output_dim)와도 동일. RNN의 용량(capacity)를 늘린다고 보면 되며, 중소형 모델의 경우 보통 128, 256, 512 등의 값을 가진다.
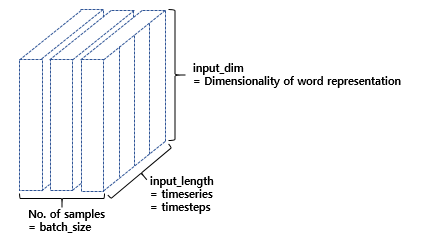
• timesteps : 입력 시퀀스의 길이(input_length)라고 표현하기도 함. 시점의 수.
• input_dim : 입력의 크기

RNN 층은 (batch_size, timesteps, input_dim) 크기의 3D 텐서를 입력으로 받는다. batch_size는 한 번에 학습하는 데이터의 개수를 말한다. 단, 여기서 설명하는 것은 RNN의 은닉층을 말한다. Fully-connected layer를 출력층으로 사용하는 것이 아니다.

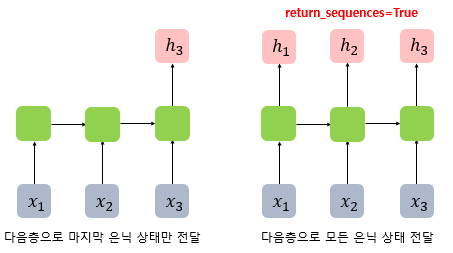
RNN 층이 앞서 설명한 입력 3D 텐서를 받아 은닉 상태를 출력하는 방법은 다음과 같다. RNN층은 사용자의 설정에 따라 두 가지 종류의 출력을 내보낸다. 메모리 셀의 최종 시점의 은닉 상태만을 리턴하고자 한다면 (batch_size, output_dim) 크기의 2D 텐서를 리턴한다. 하지만, 메모리 셀의 각 시점(time step)의 은닉 상태값들을 모아서 전체 시퀀스를 리턴하고자 한다면 (batch_size, timesteps, output_dim) 크기의 3D 텐서를 리턴한다. 이는 RNN 층의 return_sequences 매개 변수에 True를 이용하면 된다.

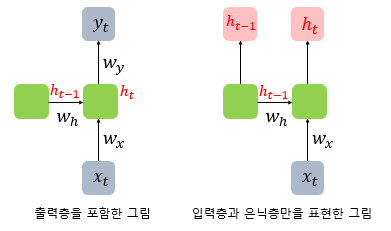
위의 그림은 time_step=3일 때, return_sequences=True를 설정했을 때와 그렇지 않았을 때의 차이이다. return_sequences=True를 선택하면 메모리 셀이 모든 시점(time_step)에 대해서 은닉 상태값을 출력하며, 별도 기재하지 않거나 return_sequences=False로 선택할 경우에는 메모리 셀은 하나의 은닉 상태값만을 출력한다. 그리고 이 하나의 값은 마지막 시점(time step)의 메모리 셀의 은닉 상태값이다.

마지막 은닉 상태만 전달하도록 하면 다 대 일(many-to-one) 문제를 풀 수 있고, 모든 시점의 은닉 상태를 전달하도록 하면, 다음층에 RNN 은닉층이 하나 더 있는 경우이거나 다 대 다(many-to-many) 문제를 풀 수 있게 된다.

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import SimpleRNN

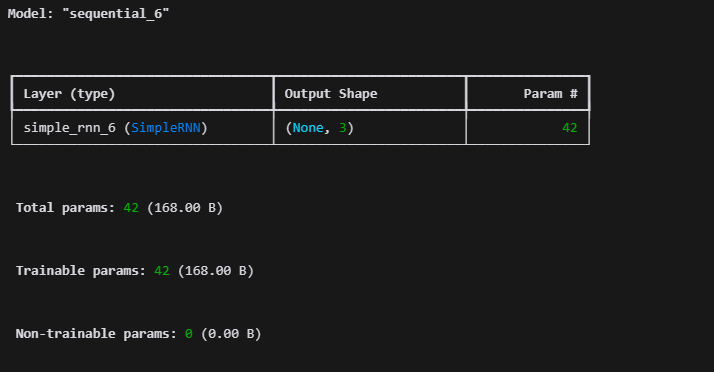
model = Sequential()
model.add(SimpleRNN(3, input_shape=[2,10]))
# model.add(SimpleRNN(3, input_length=2, input_dim=10))와 동일함.
model.summary()

3. 파이썬으로 RNN 구현하기

---

Numpy를 이용해 RNN 층을 구현해보자. 메모리 셀에서 은닉 상태를 계산하는 식은 다음과 같다.

\[h_t = thanh({W_x}x_t + {W_h}h_{t-1} + b)\]

pseudocode는 다음과 같다.

hidden_state_t = 0 # 초기 은식 상태를 0(벡터)로 초기화
for input_t in input_length: # 각 시점마다 입력 받음
    output_t = tanh(input_t, hidden_state_t) # 각 시점에 대해서 입력과 은식 상태를 가지고 연산
    hidden_state_t = output_t # 계산 결과는 현재 시점의 은닉 상태

우선 t 시점의 은닉 상태를 hidden_state_t 라는 변수로 선언하였고, 입력 데이터의 길이를 input_length로 선언하였다. 이 때, 입력 데이터의 길이는 곧 총 시점의 수(timesteps)가 된다. 그리고 t 시점의 입력값을 input_t로 선언하였다. 각 메모리 셀은 각 시점마다 input_t와 hidden_state_t(이전 상태의 은식 상태)를 입력으로 활성화 함수인 하이퍼볼릭탄젠트 함수를 통해 현 시점의 hidden_state_t를 계산한다. 아래 예시는 (timesteps, input_dim) 크기의 2D 텐서를 입력으로 받는다. 하지만 실제로 케라스에서는 (batch_size, timesteps, input_dim) 크기의 3D 텐서를 입력으로 받는다.

import numpy as np

timesteps = 10
input_dim = 4
hidden_units = 8

# 입력에 해당되는 2D 텐서
inputs = np.random.random((timesteps, input_dim))

# 초기 은닉 상태는 0(벡터)로 초기화
hidden_state_t = np.zeros((hidden_units,)) 

print('초기 은닉 상태 :',hidden_state_t) # 초기 은닉 상태 : [0. 0. 0. 0. 0. 0. 0. 0.]

Wx = np.random.random((hidden_units, input_dim))  # (8, 4)크기의 2D 텐서 생성. 입력에 대한 가중치.
Wh = np.random.random((hidden_units, hidden_units)) # (8, 8)크기의 2D 텐서 생성. 은닉 상태에 대한 가중치.
b = np.random.random((hidden_units,)) # (8,)크기의 1D 텐서 생성. 이 값은 편향(bias).

print('가중치 Wx의 크기(shape) :',np.shape(Wx)) # 가중치 Wx의 크기(shape) : (8, 4)
print('가중치 Wh의 크기(shape) :',np.shape(Wh)) # 가중치 Wh의 크기(shape) : (8, 8)
print('편향의 크기(shape) :',np.shape(b)) # 편향의 크기(shape) : (8,)

total_hidden_states = []

# 각 시점 별 입력값.
for input_t in inputs:

  # Wx * Xt + Wh * Ht-1 + b(bias)
  output_t = np.tanh(np.dot(Wx,input_t) + np.dot(Wh,hidden_state_t) + b)

  # 각 시점 t별 메모리 셀의 출력의 크기는 (timestep t, output_dim)
  # 각 시점의 은닉 상태의 값을 계속해서 누적
  total_hidden_states.append(list(output_t))
  hidden_state_t = output_t

# 출력 시 값을 깔끔하게 해주는 용도.
total_hidden_states = np.stack(total_hidden_states, axis = 0) 

# (timesteps, output_dim)
print('모든 시점의 은닉 상태 :')
print(total_hidden_states)

모든 시점의 은닉 상태 :
[[0.85575076 0.71627213 0.87703694 0.83938496 0.81045543 0.86482715 0.76387233 0.60007514]
 [0.99982366 0.99985897 0.99928638 0.99989791 0.99998252 0.99977656 0.99997677 0.9998397 ]
 [0.99997583 0.99996057 0.99972541 0.99997993 0.99998684 0.99954936 0.99997638 0.99993143]
 [0.99997782 0.99996494 0.99966651 0.99997989 0.99999115 0.99980087 0.99999107 0.9999622 ]
 [0.99997231 0.99996091 0.99976218 0.99998483 0.9999955  0.99989239 0.99999339 0.99997324]
 [0.99997082 0.99998754 0.99962158 0.99996278 0.99999331 0.99978731 0.99998831 0.99993414]
 [0.99997427 0.99998367 0.99978331 0.99998173 0.99999579 0.99983689 0.99999058 0.99995531]
 [0.99992591 0.99996115 0.99941212 0.99991593 0.999986   0.99966571 0.99995842 0.99987795]
 [0.99997139 0.99997192 0.99960794 0.99996751 0.99998795 0.9996674 0.99998177 0.99993016]
 [0.99997659 0.99998915 0.99985392 0.99998726 0.99999773 0.99988295 0.99999316 0.99996326]]

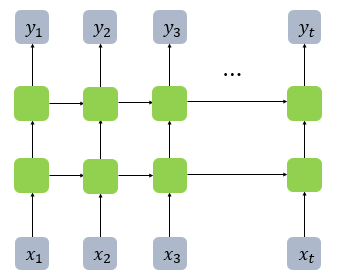
4. 깊은 순환 신경망(Deep Recurrent Neural Network, DRNN)

---

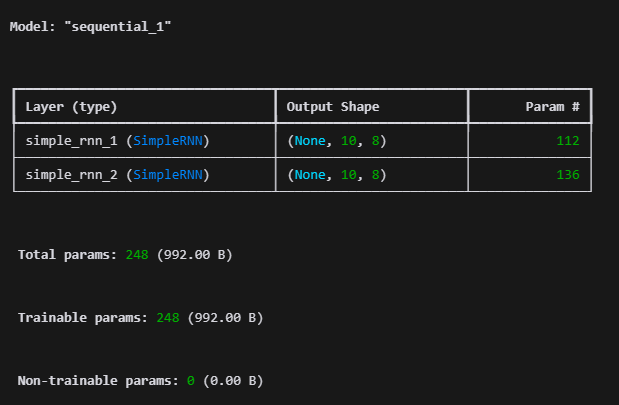
model = Sequential()
model.add(SimpleRNN(hidden_units, input_shape=[10, 5], return_sequences=True))
model.add(SimpleRNN(hidden_units, return_sequences=True))

model.summary()

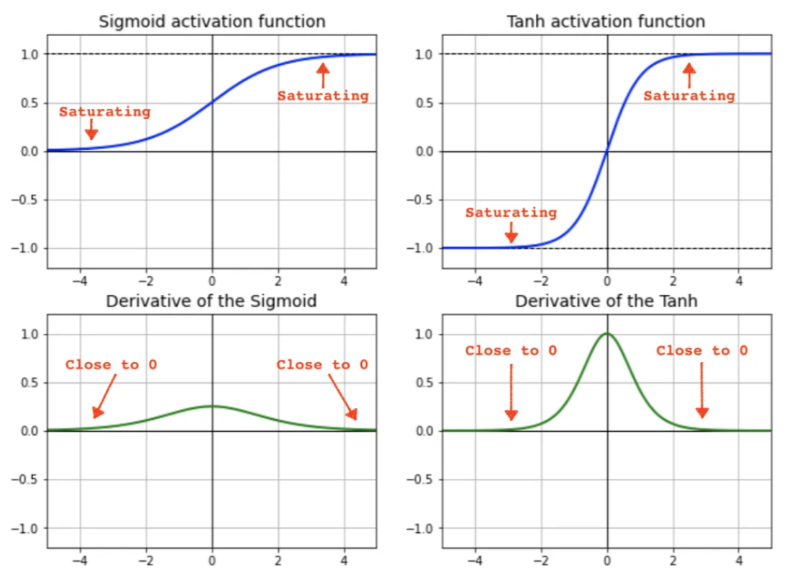
5. RNN에서 탄젠트 함수를 사용하는 이유

ReLU를 사용하면 이전 값이 커짐에 따라 오버플로우가 발생할 수 있는 문제가 있기 때문이다.

시그모이드와 tanh 함수는 특정한 범위를 넘지 못하게 되어 오버플로움 문제를 피할 수 있지만 기울기 소실 문제를 가지고 있다. 그나마 tanh 함수는 상당 부분 기울기 소실 문제를 해소할 수 있기 때문에 RNN에서 많이 사용된다.

6. RNN의 한계

1. RNN은 시퀀스 길이가 길어질수록 기울기 소실 문제(vanishing gradient problem) 가 발생할 가능성이 높다.
2. RNN은 순차적으로 처리되기 때문에 병렬 처리(parallel processing) 가 어렵다.
3. RNN은 장기 의존성(long-term dependency)을 학습하는 데 어려움 이 있다. 따라서 시퀀스가 길어질수록 이전의 정보가 희석되어 장기적인 의존성을 파악하는 데 어려움을 겪게 된다.

Reference

• wikidocs-RNN
• AI HEROES