Home PEFT 기법과 LoRA
Post
Cancel

PEFT 기법과 LoRA

Posted May 12, 2024
Preview Image
By 멍식
31 min read

최근 핫한 PEFT 기법과 그 중 LoRA 기법에 대해 알아보겠습니다.

PEFT와 LoRA

PEFT란?

Encoder

PEFT란 Hugging face에서 소개한 방법이다. Parameter-Efficient Fine-Tuning (이하 PEFT)는 사전 훈련된 거대 언어 모델을 특정 상황에 적용할 때, 대부분의 파라미터를 freeze 하고 소수의 모델 파라미터만 파인 튜닝하는 기법이다. Hugging Face에서는 LoRA, Prefix Tuning, Prompt Tuning 기법 등을 사용하기 쉽게 라이브러리로 만들어 놨다.

Huggingface PEFT 링크

위 링크에 가면 PEFT 기법과 관련된 다양한 메소드들을 볼 수 있다.

장점

  • Reduced Parameter Fine-tuning(축소된 파라미터 파인튜닝)

    사전 학습된 LLM 모델에서 대다수의 파라미터를 고정해 소수의 추가적인 파라미터만 파인튜닝하는 것이 가능

  • Overcoming Catastrophic Forgetting(치명적 망각 문제 극복)

    Catastrophic Forgetting 문제는 LLM 모델 전체를 파인 튜닝하는 과정에서 발생하는 현상인데, 이를 PEFT 기법을 활용하여 완화할 수 있다

  • Application Across Modalities(여러 모달리티 적용 가능)

    PEFT는 기존 자연어 처리 영역을 넘어서 다양한 영역으로 확장 가능하다. 스테이블 디퓨전, 컴퓨터 비전, 오디오 등 다양한 분야에 적용이 가능하다.

  • Supported PEFT Methods

    허깅페이스 라이브러리에서 다양한 방법을 지원한다. LoRA, Prefix Tuning, 프롬프트 튜닝 등 각각의 시나리오에 맞게 사용 가능하다.

LoRA란?

서론

Encoder

모델이 점점 커짐에 따라 fine-tuning 할 때 모델의 파라미터가 너무 많아지고 이에 따른 자원의 제약 등의 문제가 발생하고 있다.

저자들이 LoRA 아이디어를 얻은 논문(https://arxiv.org/abs/2012.13255) 이 있는데, 해당 논문의 저자들은 PLM(Pretrained Language Model)은 low intrinsic dimension을 가진다고 주장한다. low intrinsic dimension 이란 데이터의 고유 차원이 낮은 상황을 가리킨다. 간단히 말해, 데이터가 높은 차원에서 표현되었지만 실제로는 그보다 훨씬 낮은 차원에서 효과적으로 설명될 수 있다는 것을 의미한다. 예를 들어, 고차원의 데이터가 있을 때, 그 데이터가 실제로는 특정한 낮은 차원의 부분 공간에 놓여있을 수 있다는 것이다. 이는 보통 over-parameterized model이 가지는 특징이라고 할 수 있다. 저자들은 이를 실험을 통해 증명을 했는데 RoBERTa의 경우 오직 200 trainable parameters로 90%의 퍼포먼스를 냈다고 주장한다.

LoRA 논문의 저자들은 모델의 low intrinsic dimension에서 더 나아가 가중치 행렬도 low intrinsic dimension 파라미터를 가진다고 주장하는 것이다.

핵심 아이디어

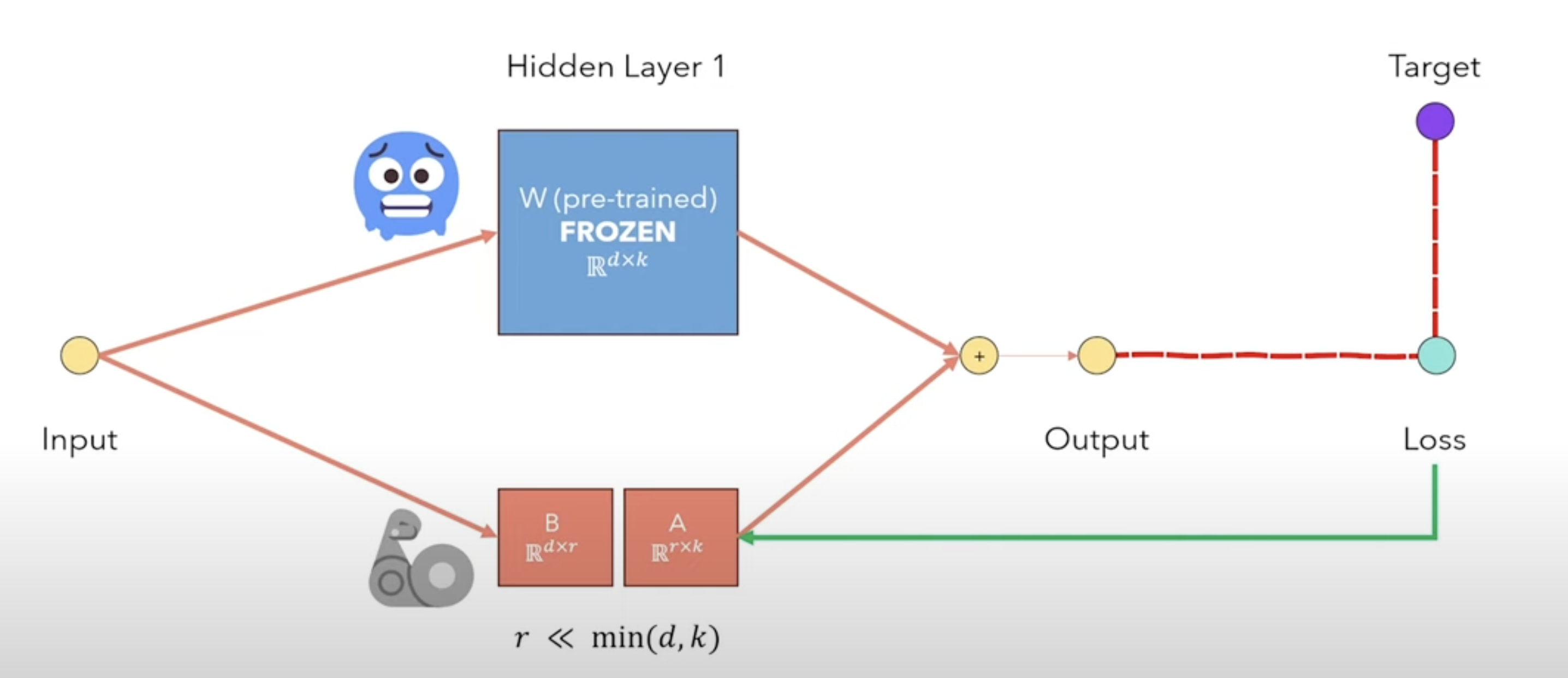
  • 훈련할 때
    • Fine Tuning할 때 Pre-trained Model의 Weights는 건드리지 않겠다. 즉, freeze 하겠다.
    • 대신 새로운 Weights를 옆에 붙여서 이 Weights만 훈련시키겠다. 이 Weights를 LoRA Weight라고 한다.
  • 추론할 때
    • 입력값을 Pre-trained Model의 Weights와 LoRA Weight 모두에 통과시킨다. 최종 결과는 Pre-trained Weight를 거친 값과 LoRA Weights를 거친 값을 더해서 사용한다.

수식으로 공부해보기

Encoder

  1. 기존의 LLM 모델을 하나의 확률함수 PΦ(y bar x)라고 한다.
  2. fine-tuning 과정에서 LLM이 튜닝되는 Φ가 최적화 되는 식은 식(1) 처럼 표현된다.
    1. Log-likelihood function으로 문제를 해결할 때 가장 적합한 파라미터 Φ가 나올 확률을 최대화하는 것이다.
    2. 직관적으로 backpropagation 할 때의 모델을 나타내면, Φ = Φ0 + ΔΦ 가 된다.
  3. 식(1)에 근거하여 만약 accumulated gradient values(ΔΦ)를 기존보다 훨씬 적은 파라미터인 Θ로 치환하여 ΔΦ(Θ)로 나타내면 식(2)로 바뀌게 된다.
    1. 즉, 기존의 log-likelihood 문제에서 모델이 backpropagation 과정에서 이용되는 파라미터 연산 문제를 더 적은 파라미터 Θ로 치환하여 풀겠다는 의미.

Whisper에 PEFT 기법 적용하기

PEFT 도입 계기

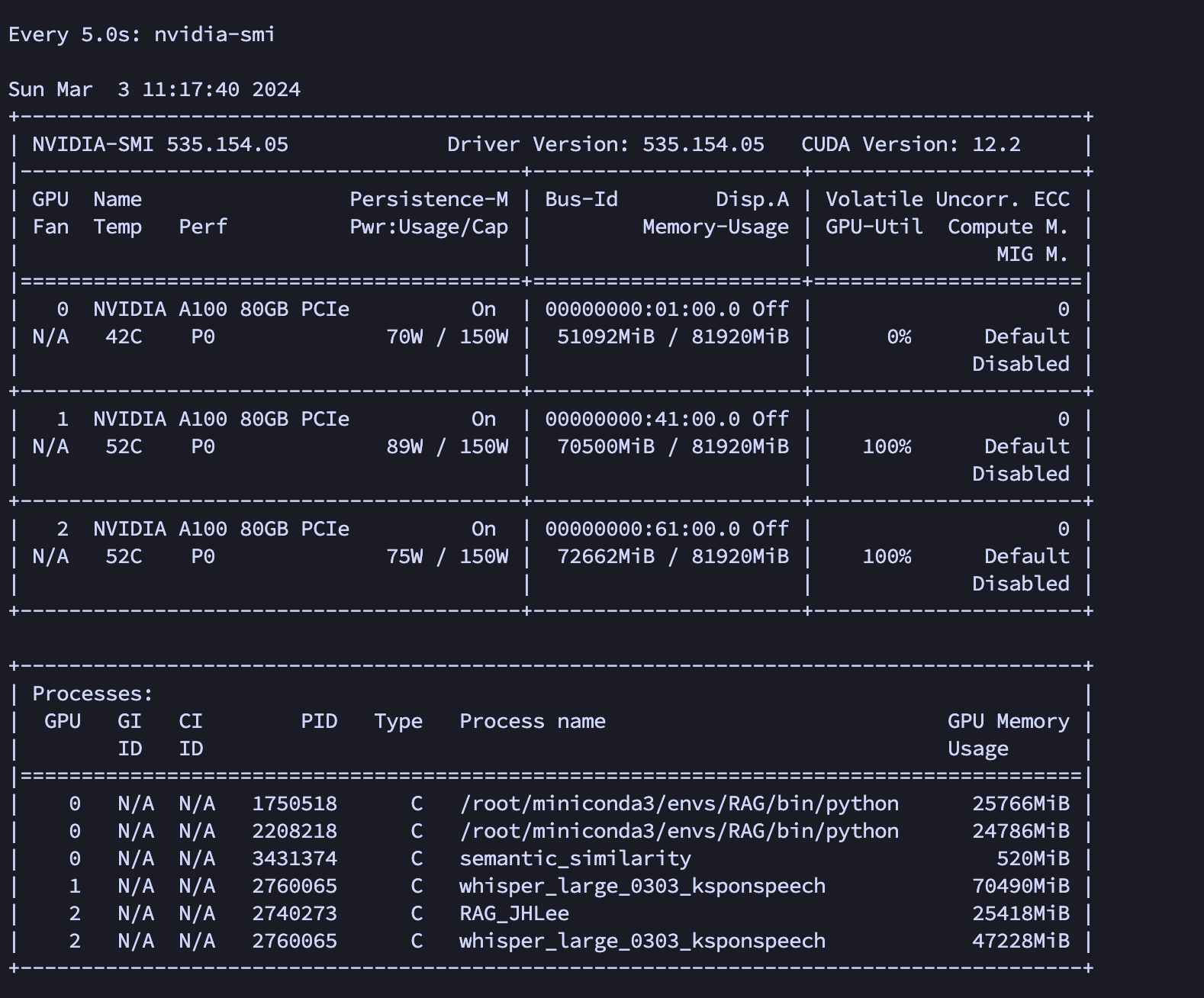
Encoder

(위 이미지에서 whisper_large_0303_ksponspeech라고 쓰인게 파인튜닝하고 있는 Whisper 모델이다.)

  • 모델 : whisper-large-v2
  • 학습 데이터 : 1만개
  • 학습 데이터 시간 : 15h 26m 47s
  • 모델 학습 시간 : 약 63시간(약 2.5일)
  • 배치 사이즈 : 8
  • Gradient Accumulation : 4
  • 스탭(save_points) : 100
  • 사용 gpu 메모리 : 약 110G

네.. 이거 못합니다🥲 그래서 찾다보니 LoRA 기법을 Whisper에도 적용할 수 있다는 것을 알게됨.

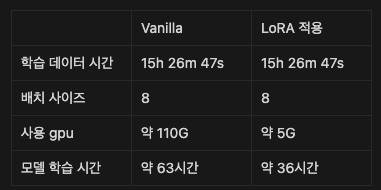
비교

Encoder

  • 사용 gpu 메모리가 정말 어마어마하게 줄은 것을 확인
  • 학습 시간 또한 감소(물론 학습 시간은 의미 x)

그래서 작정하고 배치사이즈 늘려서 학습시켜봤더니

  • 모델 : whisper-large-v2 + peft 기법 적용
  • kspon 데이터 : 60만개
  • 학습 데이터 : 54만개
  • 평가 데이터 : 6만개
  • 학습 데이터 시간 : 840h 32m 45s
  • 모델 학습 시간 : 약 400시간(약 15일) + 알파(다른 모델 학습이 진행되면 학습 시간이 늘어남)
  • 에폭 : 10
  • 배치 사이즈 : 256
  • Gradient Accumulation : 2
  • 스탭 : 100
  • 사용 GPU : 약 95G(95000MiB)
  • CER : 6프로(0.06)

배치 사이즈도 늘릴 수 있었고 CER도 0.06으로 좋게 나온 것을 확인.

✅ 학습 시간이 의미가 없다?

Whisper 모델을 fine-tuning 할 때 학습 시간 이 아닌 step 에 초점을 두었습니다. 왜냐하면 워낙의 큰 모델이라 학습 데이터를 아무리 적게한들 fine-tuning 시간이 오래 걸렸기 때문입니다. 따라서 step 을 100으로 설정해두고 100step 마다 성능 개선이 어느정도 되는지를 관찰하였습니다.

LoRA에 관하여

그래서 원리가 뭔데?

기본 개념 정리

  • 행렬의 랭크(Rank)
    • 행렬의 열 또는 행 중에 다른 행 또는 열의 정수배가 아닌 즉, 선형 독립 인 행 또는 열의 최대 개수.
    • 선형 독립이라는 것은 어떤 벡터가 다른 벡터들의 선형 조합으로 표현될 수 없다는 것을 의미
    • 예를 들어, 행렬 A의 Rank가 r 이라면, 이 행렬은 r개의 선형 독립인 행 또는 열 벡터를 가지고 있다는 의미
    • Full Rank 행렬
      • 행렬이 가능한 최대 랭크를 갖는 경우를 말함. 이는 행렬의 행 전체 또는 열 전체가 선형 독립인 경우를 말함
      • 예를 들어, m x n 크기의 행렬에서 행 전체 랭크(full row rank)를 갖는다면 이는 행렬의 모든 행 벡터들이 선형 독립임을 의미하며, 이 경우 행렬의 랭크는 m이다. 이는 열의 경우에도 마찬가지이다. 만약 행렬이 열 전체 랭크(full column rank)를 갖는다면, 이는 행렬의 모든 열벡터들이 선형 독립임을 의미하며, 이 경우 행렬의 랭크는 n이다.
      • 행렬이 전체 랭크(full rank)를 갖는다고 할 때, 이는 행렬이 정방행렬(square matrix, m=n)인 경우에 해당하며 모든 행과 열이 선형 독립인 경우를 의미한다. 전체 랭크를 갖는 행렬은 역행렬을 가지며, 따라서 가역(invertible) 또는 비특이(non-singular)이라고 불린다.
    • Low-Rank 행렬
      • 행렬의 Rank가 행렬의 행 수나 열 수보다 작은 경우. 즉, 행렬의 모든 정보나 구조가 상대적으로 적은 수의 행 또는 열 벡터들에 의해 완전히 표현될 수 있는 경우
      • Low-Rank 행렬은 종종 두 개 또는 그 이상의 더 작은 행렬의 곱으로 분해될 수 있다. 예를 들어, m x n 행렬 A가 Rank r인 경우, A는 m x r 행렬과 r x n 행렬의 곱으로 표현될 수 있다.
  • 행렬 분해(Matrix Factorization)
    • 복잡한 행렬을 더 간단하거나 해석하기 쉬운 여러 행렬의 곱으로 나타내는 과정을 의미한다. 이 방법은 데이터의 숨겨진 특징을 발견하고, 차원을 축소하며, 데이터를 압축하는 데 유용하게 사용된다

🤔 이게 LoRA에서 어떻게 쓰이냐?

행렬의 Rank는 선형적으로 독립적인 행 또는 열의 개수이다.

즉, 다른 행이나 열에 정수를 곱해서 만들 수 없는 고유한 행 또는 열의 개수이다.

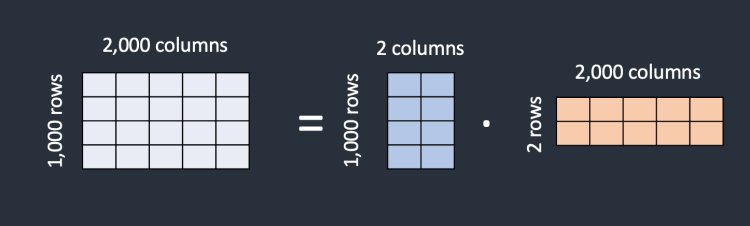
다음과 같은 2 x 3 크기의 행렬 x 가 있다고 할 때,

\[\begin{bmatrix}1&2&3\\3&6&9\\ \end{bmatrix}\]

두 번째 행이 첫 번째 행의 세 배라는 것을 알 수 있는데, 이는 행렬 x에 고유 행이 하나만 있으므로 랭크 1 행렬이 된다는 것을 의미한다. 따라서 행렬 x는 아래처럼 두 개의 작은 행렬인 A와 B로 각각 크기가 2x1과 1x3인 두 개의 작은 행렬로 분해할 수 있다.

\[\begin{bmatrix}1\\3\\ \end{bmatrix} * \begin{bmatrix}1&2&3\\\end{bmatrix} = \begin{bmatrix}1&2&3\\3&6&9\\ \end{bmatrix}\]

이제 full-rank 행렬 x 대신 두 개의 low-rank 행렬 A와 B로 표현할 수 있다.

Encoder

이걸 식으로 나타내면 다음과 같다.

\[h = W_0 x + \Delta W_x = W_0 x + BAx\]

여기서

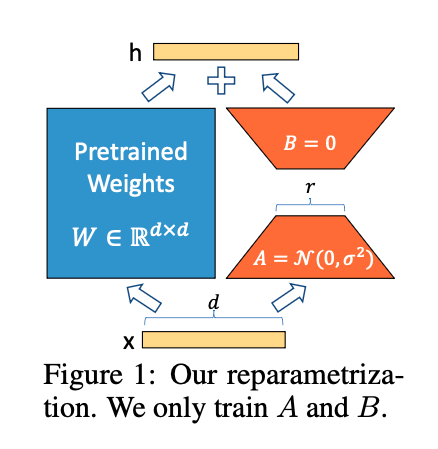
\[W \approx BA\]

로 표현될 수 있으며 BA는 원래 가중치 행렬 W와 같은 차원을 가지지만 더 낮은 랭크를 갖는다. h 는 현재 레이어의 출력, W_0 는 사전 학습된 원래 가중치로 학습 중 고정되며, 델타W 는 원래 가중치에 추가되는 가중치로 학습 중 업데이트 된다. BA 는 low-rank 가중치, x는 입력이다.

A에는 무작위 가우시안 초기화를 사용하고 B에는 0을 사용하므로 훈련 시작 시 $\Delta W = BA$ 는 0이다.

Whisper large-v3 모델을 예로 들자. 이 모델의 파라미터 개수는 1550M 즉, 15.5억개의 가중치를 갖는 N x M 크기의 가중치 행렬이 있는 것이다. 그러면 N과 M보다 작은 수 K를 선택하여 N x K와 K x M 크기를 갖는 새로운 가중치 행렬 UA와 UB를 생성한다. UA x UB는 N x M과 똑같은 크기의 행렬을 생성하지만 UA와 UB 행렬에 저장된 파라미터 개수는 줄게된다. 여기서 K는 튜닝해야하는 하이퍼 파라미터로, K가 작을수록 LLM 모델의 성능이 떨어진다.

이제 위스퍼 모델의 N x M 가중치 행렬 W 를 업데이트 하는 대신 UA x UB 가중치 행렬 델타 W를 업데이트한다. Y = m x W + B 방정식에서 가중치 W와 바이어스 B는 튜닝이 되지 않는다. 모델을 학습시키면 W는 업데이트된 가중치 Wu가 된다. 여기서 Wu는 W+델타W를 의미한다. 델타W는 기본 가중치 W에 대한 업데이트된 가중치이다.

\[Y = m x Wu + B = m(W+\Delta W) + B = m(W+UA * UB) + B\]

W를 학습시키는 대신 델타 W즉, UA * UB만 학습시킨 후 , W에 더해준다.

위 그림에서 A는 랜덤 가우시안 초기화, B는 0으로 초기화 되서 ∆W는 학습 초기에는 0이다. ∆W는 α/r로 스케일링 한다. (α는 r에서의 constant) Adam으로 최적화할 때 초기화를 적절히 스케일링 했다면, α를 튜닝하는 것은 lr을 튜닝하는 것과 같다. 결과적으로 단순히 α를 우리가 시도한 첫 번째 r로 설정하고 조정하지 않는다.

Encoder

이미지 링크

즉, Pre-trained weight은 frozen 하고 LoRA weight만 업데이트하는 것이다.

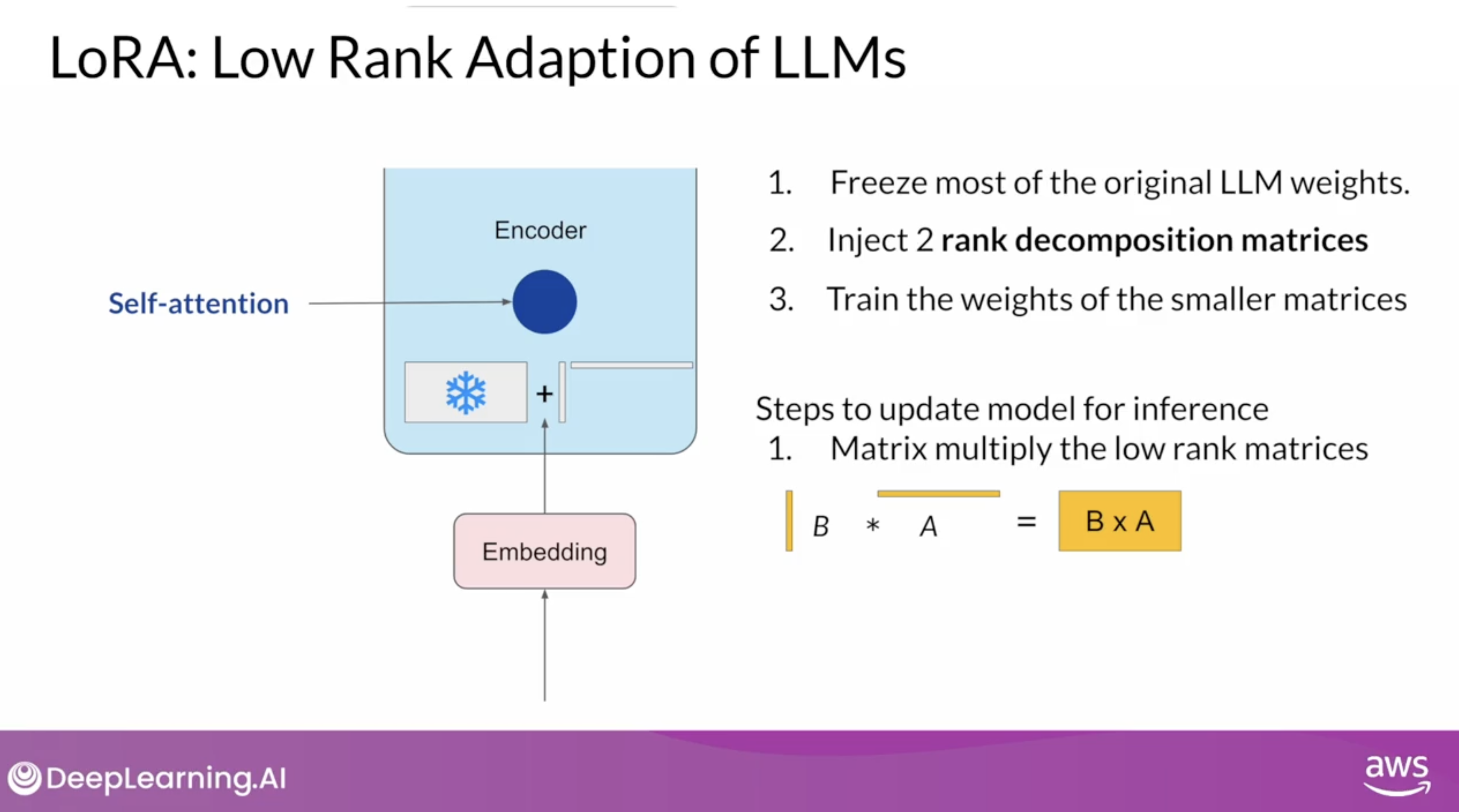
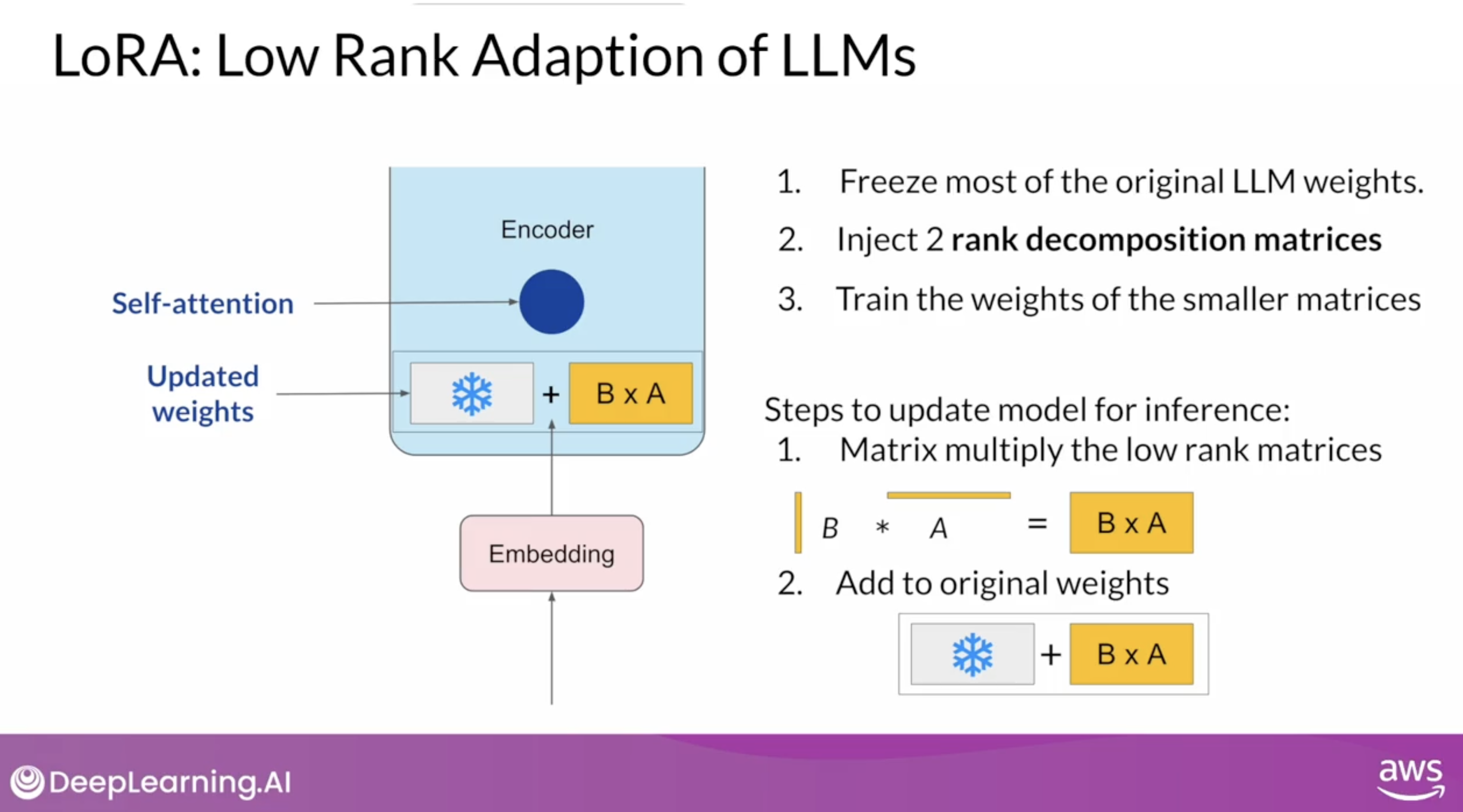
아래 코세라에 있는 LoRA 강의 영상을 캡쳐해왔다. 이미지를 보면 정말 이해가 잘된다.

Encoder

원래 모델의 파라미터들은 고정하고, read만 수행한다. 이 때, back-propagation은 수행하지 않는다.

Encoder

Encoder

한 쌍의 low-rank decomposition 행렬을 만들고, 파인 튜닝을 한다. 이 때, 만들지는 low-rank decomposition 행렬은 원래 모델의 가중치 행렬과 차원이 같도록 설정한다.

Encoder

인퍼런스 과정에서는 한 쌍의 low-rank decomposition 행렬을 곱하여 frozen 해놓은 원래 모델의 파라미터와 같은 크기의 행렬을 만든 다음 두 행렬을 더하여 업데이트한다. 강의에서 LoRA 기법은 주로 셀프 어텐션 레이어에 적용된다고 한다.

기존 Adapter와 LoRA의 차이

Encoder

기존에 있던 Adapter

Encoder

LoRA

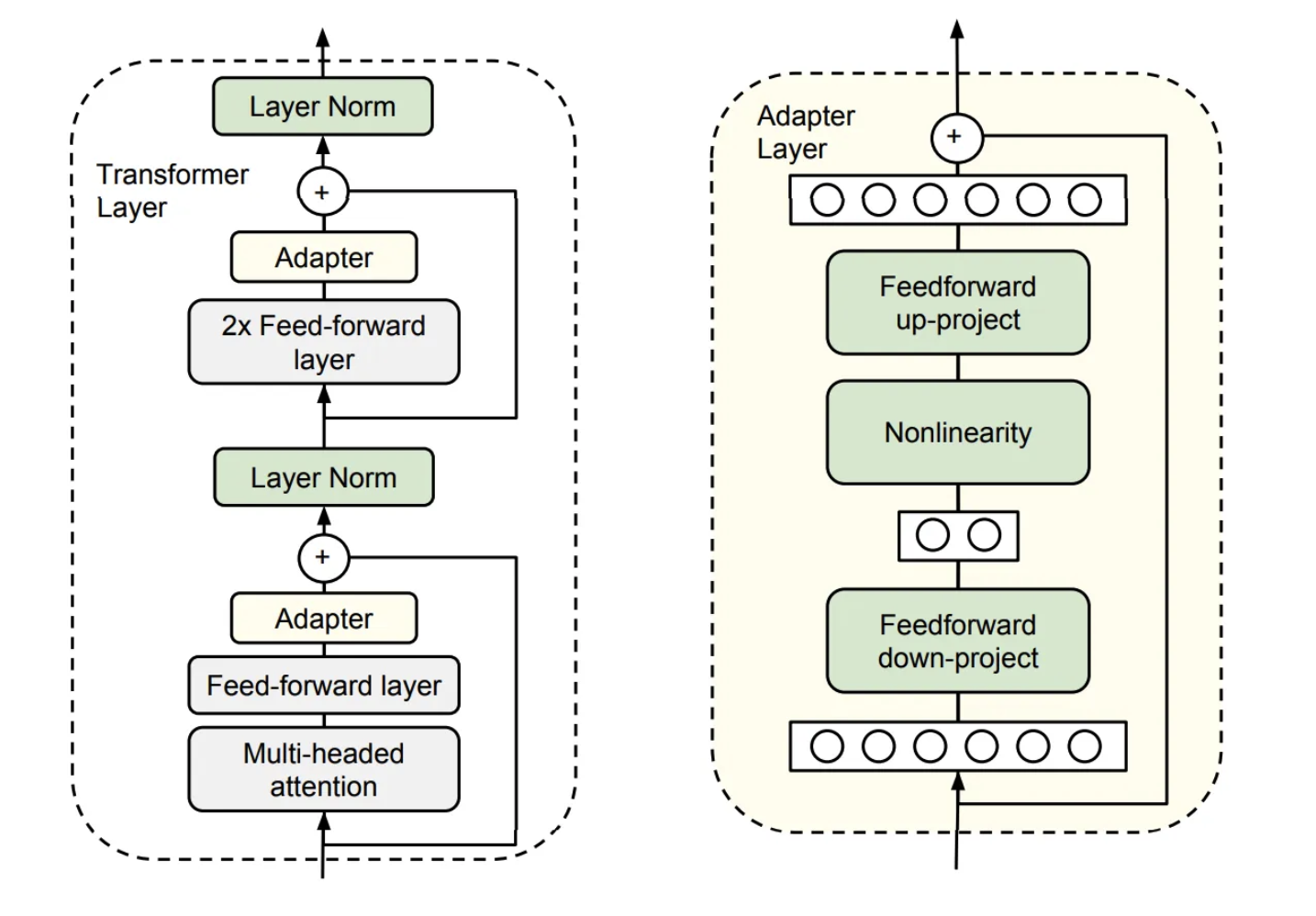
  • 주황색 부분이 adapter 라는 layer다. 이 부분을 transformer block 에 추가해주어 이 부분만 학습하는 것으로 기존 fine-tuning을 대체하는 것.
  • 기존에 adapter 기법이 있었지만 이 것으로는 충분하지 않음. 실제 논문 소제목에도 “Aren’t Existing Solutions Good Enough?” 라고 되어있음.
  • 그렇다면 기존 adapter 는 무엇이 단점이었는가?
    • 기존 adapter 는 transformer layer 사이에 adapter layer를 일정 Layer 개수마다 1개씩 배치하고 fine tuning 단계에서 adapter layer만 학습한다.
    • 오른쪽 그림 adapter layer를 자세히 나타낸 것인데, 여기서 feedforward up-project와 feedforward down-project만 학습한다.
    • 문제점은 왼쪽 그림을 보면 adapter의 연산이 이루어지려면 앞서 multi-headed attention의 연산이 이루어져야한다. 즉, sequentially 하게 연산이 진행되기 때문에 inference latency 가 추가적으로 발생한다.

🤔 그렇다면 기존 adapter와 LoRA의 차이는 뭘까?

Encoder

  • 존 Adapter와 LoRA의 그림은 정말 비슷해보인다. 기존 adapter에도 r차원으로 down projection 하는 매트릭스가 있고 그걸 다시 up projection 해주는 메트릭스가 있다
  • ‘pre-trained language models have a low “instrisic dimension” and can still learn efficiently despite a random projection to a smaller subspace’
    • intrinsic dimension : 모델이 실제로 정보를 표현하는데 필요한 차원의 수
    • random projection : 고차원 데이터를 보존하면서 저차원으로 차원의 수를 줄이는 것.
  • 차이는 바로 LoRA 에서는 r차원으로 낮추면서도, 데이터를 효과적으로 압축할 수 있다는 것. 그리고 이걸 pretrained modeld에만 적용하는 것이 아닌 가중치 행렬에도 적용하는 것!!

그래서 구해진 가중치를 어떻게 하는데?

  • Applying LoRA to Transformer : 논문에선 학습 가능한 매개변수의 수를 줄이기 위해 신경망에서 어떤 가중치 행렬의 부분집합에 적용이 가능할지 고민하다 저자는 parameter-efficiency를 위해 downstream task에 대해서 attention weight만 adapting하고 MLP(Multi Layer Perceptron)에서는 동결시킴
  • 즉, 구해진 새로운 가중치 행렬을 attention weight에 대해 더하거나 빼는 식으로 사용가능.
  • 따라서 논문에서 언급했듯이, 새로운 태스크에 대해 기존 모델은 냅두고 갈아 끼우는 것이 가능하다.

그렇다면 적절한 r 값이 뭐야?

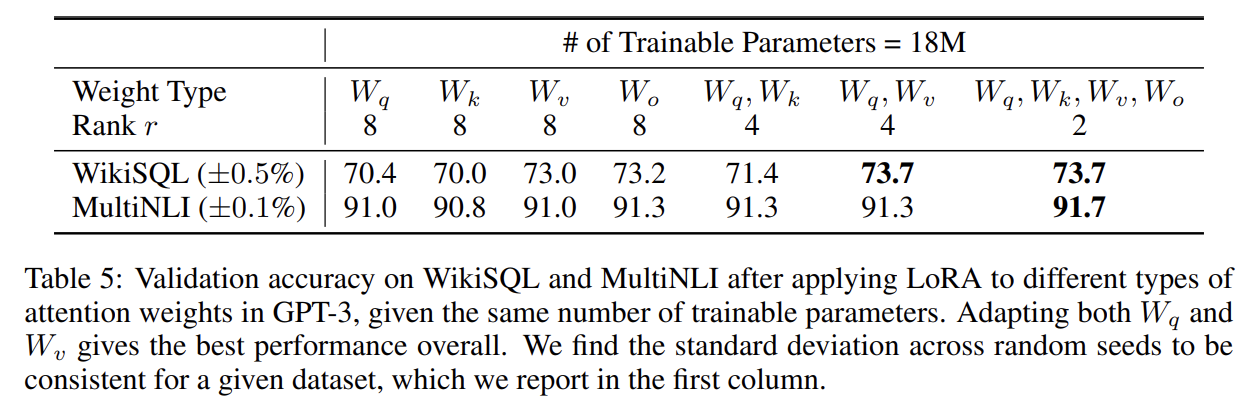
Encoder

모든 파라미터에 적용하는 것 보다 W_q와 W_v에만 적용하는 것이 가장 좋은 성능을 보임을 확인할 수 있다.

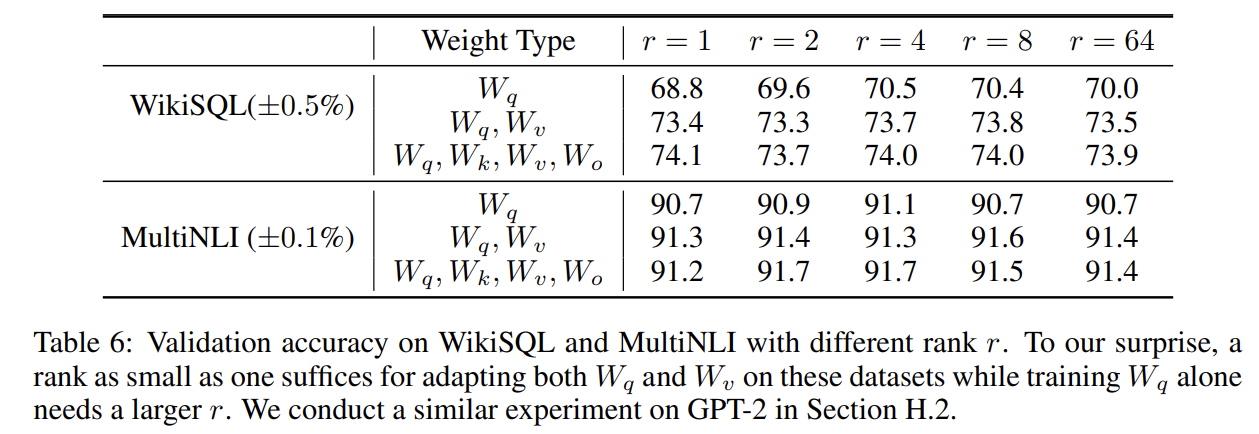
Encoder

이때, r 이 증가한다고 더 의미 있는 결과를 도출해내는 것은 아님. 따라서 낮은 r 값으로도 충분하다는 것을 증명.

❕ 여러 번 실험을 통해 적절한 r 값을 찾아야한다.

예시

예를 들어, 멍식이란 모델이 가중치가 400000 x 100000 행렬을 갖는데 랭크가 10이라면 가중치는 400000 x 10 크기와 10 x 400000 크기의 행렬인 UA와 UB로 분해된다.

파인 튜닝을 할 경우엔 전체 파라미터인 40B(400000 x 100000 = 400억개)를 업데이트하는 반면 LoRA를 사용하면 AU의 크기 400만개(400000 x 10) 와 UB의 크기 100만개 (10 x 100000)만 업데이트하면 된다. 즉, 기존 400억개보다 적은 500만 개의 파라미터만 업데이트하면 되므로 파라미터의 개수가 약 98.86% 감소하여 계산하는데 걸리는 시간이 줄게 된다!!

Encoder

실제로 Whisper large-v2 모델에 적용했을 때 학습 가능한 파라미터는 약 1% 로 나온다.

양자화(Quantization)

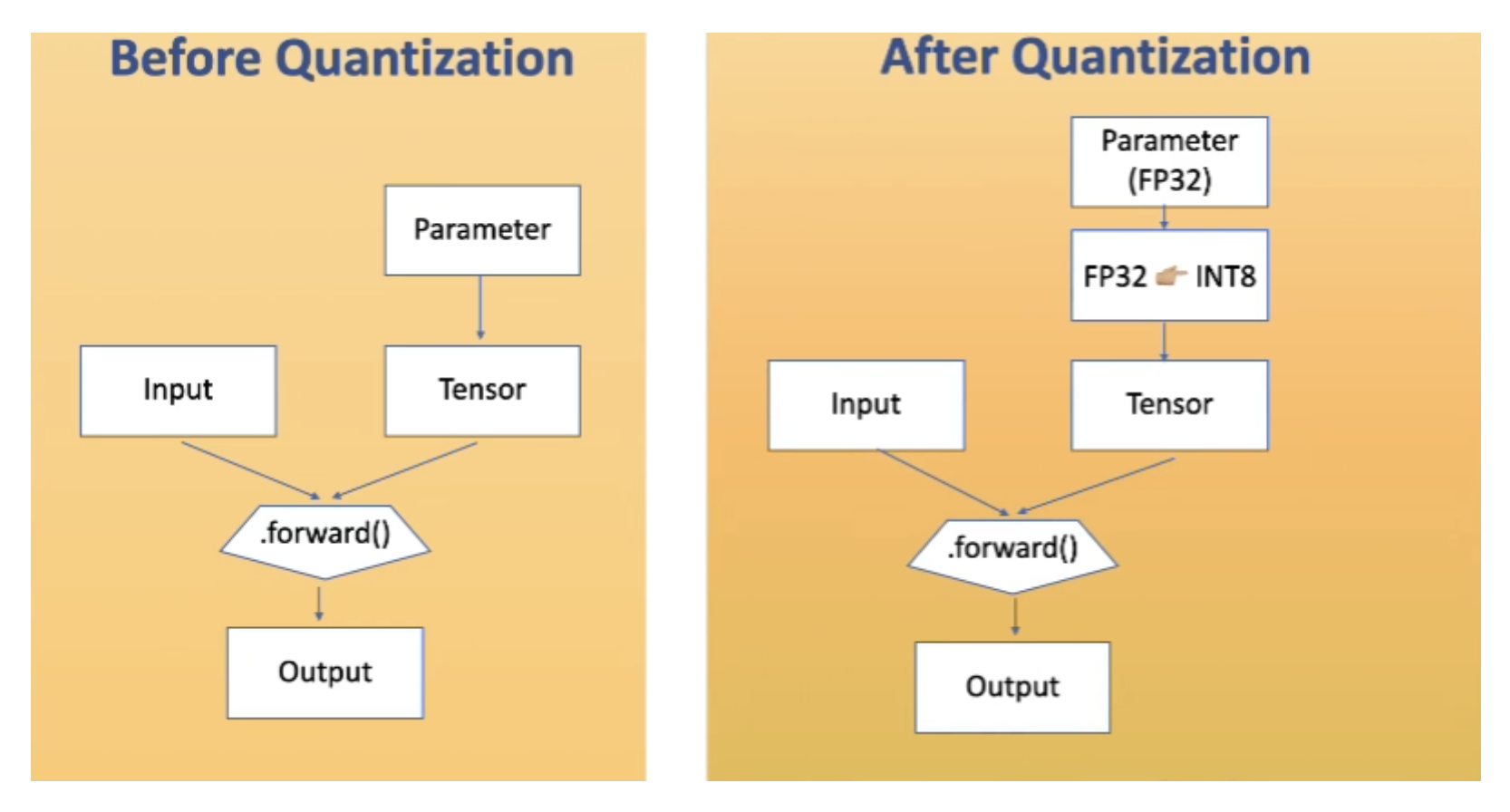
위스퍼 파인튜닝에는 LoRA 기법 + 양자화 기법 이 적용되었다. 이를 QLoRA라고 한다. 양자화란 실수형 변수(floating-point type)를 정수형 변수(integer or fixed point)로 변환하는 과정이다.

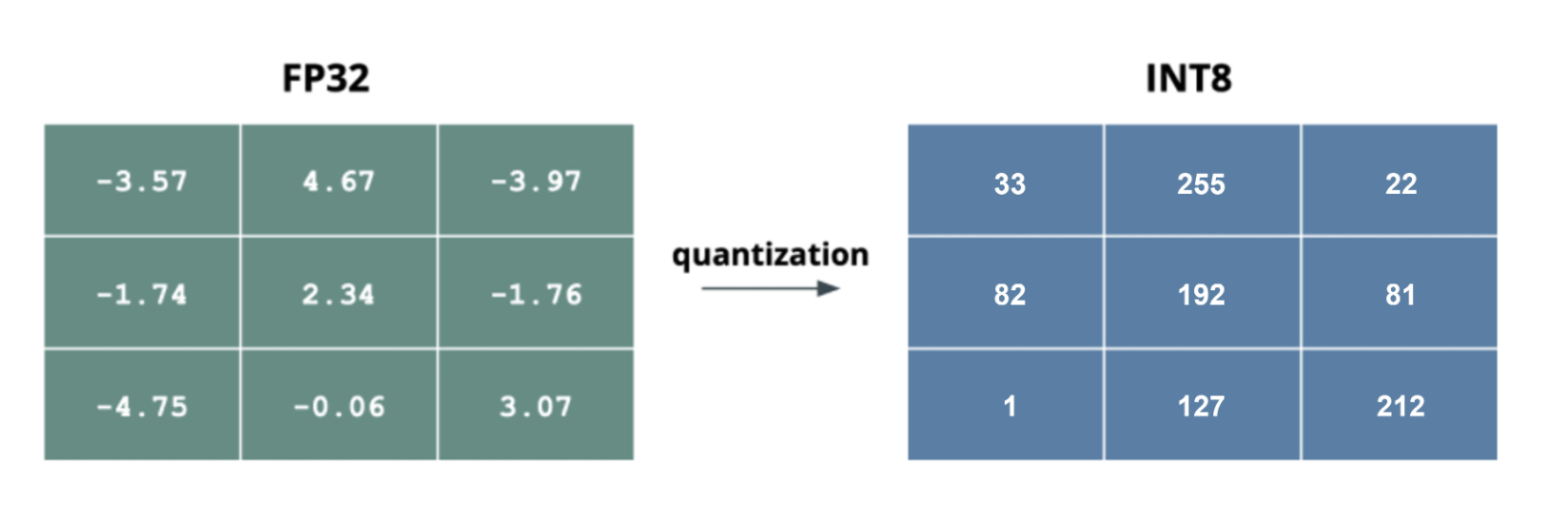
Encoder

그리고 FP32 타입의 파라미터를 INT8 형태로 변환하는게 일반적이라고 한다.(정수형 변수의 bit 수를 N배 줄이면 곱셈 복잡도는 N * N 배로 줄어든다)

Encoder

  • FP32 대신 INT8 을 사용한다면 보통
    • 모델 사이즈 : 1 / 4 이 되고
    • 추론 속도 : 2 ~ 4배 빨라지며
    • 용량 : 2 ~ 4배 가벼워진다고 한다.

FP32 에서 INT8 로 변환 시 정보 손실이 발생하기 때문에 역으로 INT8 에서 FP32 로 역변환하면 그대로 변환되지 않는다. 이 때 발생하는 Error를 Quantization Error 라고 하며 이 Error를 줄이는 것이 좋은 Quantization 알고리즘이다.

코드

config

1
2
3

from peft import LoraConfig, PeftModel, LoraModel, LoraConfig, get_peft_model

config = LoraConfig(r=32, lora_alpha=64, target_modules=["q_proj", "v_proj"], lora_dropout=0.05, bias="none")
  • r : update 되는 가중치 matrix의 rank. 작을수록 trainable param이 적어짐. 작을수록 많이 압축
  • target_modules : LoRA로 바꿀 모듈. 앞서 언급했듯이 Transformer 모델은 attention block에만 적용된다. 위 코드에서도 q와 v에만 적용.
  • lora_alpha : LoRA scaling factor. scaling 값이 lora_alpha / r 로 들어간다.
    • 스케일링 펙터 : lora_alpha는 LoRA 모듈에 의해 생성된 델타 가중치 행렬의 크기를 조정하는 스케일링 팩터로 작동한다. LoRA에서 델타 가중치는 상대적으로 작은 크기의 행렬을 사용해 계산되며, 이를 통해 대형 모델의 가중치에 변화가 가해진다
    • 가중치 업데이트의 제어 : 학습 중에 LoRA 모듈이 전체 모델에 가하는 영향력을 조절하는 역할을 합니다. lora_alpha의 값이 크면 LoRA 모듈에 의해 가해지는 가중치 변경의 효과가 커지며, 반대로 작으면 효과가 줄어듭니다.
    • 학습 안정성 : lora_alpha를 적절한 값으로 설정함으로써 델타 가중치 업데이트가 너무 과도하게 적용되거나, 반대로 너무 미미하게 적용되는 것을 막을 수 있습니다.
  • bias : bias도 학습할 것인지 선택. [’none’, ‘all’, ‘lora_only’] 가 있다. default 값은 ‘non’ 이고 이를 켜면 weight 뿐만 아니라 bias도 lora로 처리한다.
  • lora_dropout : LoRA 모듈이 특정 입력 피처에 과도하게 의존하는 것을 방지한다. 이를 통해 모델이 입력 데이터에 과적합 되는 것을 줄인다.

구현체

  1. get_peft_model

모델 불러오기

1

model = get_peft_model(model, config)
  1. LoRA Layer

모든 Layer를 A와 B로 관리하고 있다

1
2
3
4
5

class LoraLayer(BaseTunerLayer):
    # All names of layers that may contain (trainable) adapter weights
    adapter_layer_names = ("lora_A", "lora_B", "lora_embedding_A", "lora_embedding_B")
    # All names of other parameters that may contain adapter-related parameters
    other_param_names = ("r", "lora_alpha", "scaling", "lora_dropout")
  1. Linear

Q. 기존 weight와 LoRA weight을 어떻게 merge 하는거지?

A. proj_k, proj_q와 같은 모듈 key에 해당하는 레이어 weight의 get_delta_weight output과 기존의 weight을 단순히 더해주는 형태이다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66

def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
        """
        Merge the active adapter weights into the base weights

        Args:
            safe_merge (`bool`, *optional*):
                If True, the merge operation will be performed in a copy of the original weights and check for NaNs
                before merging the weights. This is useful if you want to check if the merge operation will produce
                NaNs. Defaults to `False`.
            adapter_names (`list[str]`, *optional*):
                The list of adapter names that should be merged. If None, all active adapters will be merged. Defaults
                to `None`.
        """
        adapter_names = check_adapters_to_merge(self, adapter_names)
        if not adapter_names:
            # no adapter to merge
            return

        for active_adapter in adapter_names:
            if active_adapter in self.lora_A.keys():
            # key ex) 'proj_k', 'proj_q' ...
                base_layer = self.get_base_layer()
                if safe_merge:
                    # Note that safe_merge will be slower than the normal merge
                    # because of the copy operation.
                    orig_weights = base_layer.weight.data.clone()
                    delta_weight = self.get_delta_weight(active_adapter)
                    ##############################################################
                    # base model의 weight과 lora 결과를 합치는 부
                    if not self.use_dora[active_adapter]:
                        orig_weights = orig_weights + delta_weight
                    ##############################################################
                    else:
                        # handle dora
                        # since delta_weight already includes scaling, set it to 1 here
                        weight_norm = self._get_weight_norm(orig_weights, delta_weight, scaling=1).detach()
                        # We need to cache weight_norm because it has to be based on the original weights. We
                        # cannot calculate it on the fly based on the merged weights when unmerging because its a
                        # different value
                        self._cache_store(f"{active_adapter}-weight_norm", weight_norm)
                        dora_factor = self.lora_magnitude_vector[active_adapter] / weight_norm
                        orig_weights = dora_factor.view(-1, 1) * (orig_weights + delta_weight)

                    if not torch.isfinite(orig_weights).all():
                        raise ValueError(
                            f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
                        )

                    base_layer.weight.data = orig_weights
                else:
                    delta_weight = self.get_delta_weight(active_adapter)
                    if not self.use_dora[active_adapter]:
                        base_layer.weight.data = base_layer.weight.data + delta_weight
                    else:
                        # handle dora
                        # since delta_weight already includes scaling, set it to 1 here
                        weight_norm = self._get_weight_norm(base_layer.weight, delta_weight, scaling=1).detach()
                        # We need to cache weight_norm because it has to be based on the original weights. We
                        # cannot calculate it on the fly based on the merged weights when unmerging because its a
                        # different value
                        self._cache_store(f"{active_adapter}-weight_norm", weight_norm)
                        dora_factor = self.lora_magnitude_vector[active_adapter] / weight_norm
                        new_weight = dora_factor.view(-1, 1) * (base_layer.weight.data + delta_weight)
                        base_layer.weight.data = new_weight

                self.merged_adapters.append(active_adapter)

Reference

PEFT
oeft adapter lora
Contents