밑바닥부터 다시 개념 정리를 해봅시다..
개념 끄적이기..
1. 국소적 계산과 계산 그래프
계산 그래프의 특징은 국소적 계산 을 전파함으로써 최종 결과를 얻는 다는 점에 있다. 국소적이란 ‘자신과 직접 관계된 작은 범위’ 라는 뜻이다. 결국 전체에서 어떤 일이 벌어지든 상관없이 자신과 관계된 정보만으로 결과를 출력할 수 있다는 것이다.
그렇다면 왜 계산 그래프 로 푸는 것일까?
바로 국소적 계산 을 할 수 있다는 것이다. 전체가 아무리 복잡해도 각 노드에서는 단순한 계산에 집중하여 문제를 단순화할 수 있다. 그리고 역전파를 통해 ‘미분’을 효율적으로 계산할 수 있다. 예를 들어, 사과 가격이 오르면 최종 금액에 어떤 영향을 끼치는지를 알고 싶다고 하자. 이는 ‘사과 가격에 대한 지불 금액의 미분’을 구하는 문제에 해당한다. 이는 계산 그래프에서 역전파를 하면 구할 수 있다.
2. 곱셈 노드 역전파
곱셈 노드 역잔파는 상류의 값에 순전파 때의 입력 신호들을 서로 바꾼값을 곱해서 하류로 보낸다.
\[y = x_1 * x_2\] \[dx_1 = dy * x_2\]여기서 $dx_1$ 는 $x_1$에 대한 그라디언트이고 dy 는 상류에서 전달된 것이다.
덧셈의 역전파에서는 상류의 값을 그대로 흘려보내서 순방향 입력 신호의 값은 필요하지 않다. 그러나 곱셈의 역전파는 순방향 입력 신호의 값이 필요하다. 그래서 곱셈 노드를 구현할 때는 순전파의 입력 신호를 변수에 저장해둔다.
3. 가중치 초기화 기법
weight decay 즉, 가중치 감소란 가중치 매개변수의 값이 작아지도록 학습하는 방법이다. 가중치 값을 작게 하여 오버피팅이 일어나지 않게 하는 것이다. 가중치의 초깃값을 모두 0으로 설정하면 안되는 이유는 오차역전파법에서 모든 가중치의 값이 똑같이 갱신되기 때문이다.
- sigmoid & tanh : Xavier 초깃값
- ReLU : He 초깃값
이렇게 사용해서 가장 적절한 초깃값으로 가중치를 갱신해 나가는게 좋다.
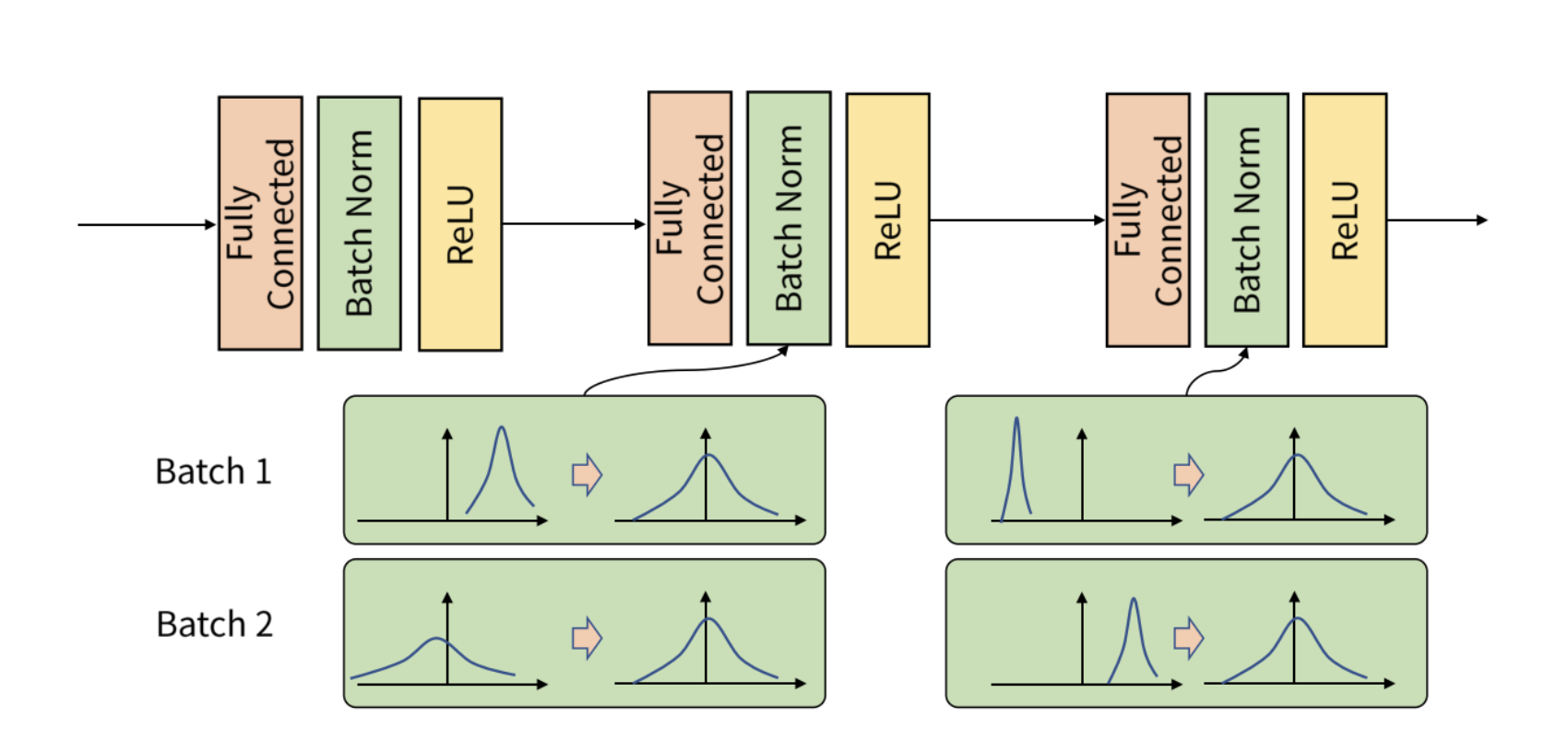
4. Batch Normalization(배치 정규화)
가중치 초기화 기법은 가중치의 초깃값을 적절히 설정하면 각 층의 활성화값 분포가 적당히 퍼지면서 학습이 원활하게 수행됨을 알아낸 것이다. 그렇다면 각 층이 활성화를 적당히 퍼뜨리도록 ‘강제’해보면 어떨까? 배치 정규화가 이 아이디어에서 출발한 방법이다.
배치 정규화는 다음과 같은 장점을 가진다.
- 학습을 빠르게 진행할 수 있다.
- 초깃값에 크게 의존하지 않는다
- 오버피팅을 억제한다.
배치 정규화의 기본 아이디어는 각 층에서의 활성화값이 적당히 분포되도록 조정하는 것이다. 그래서 데이터 분포를 정규화하는 배치 정규화 계층을 신경망에 삽입한다. 배치 정규화는 학습 시 미니배치를 단위로 정규화한다. 구체적으로는 데이터 분포가 평균이 0, 분산이 1이 되도록 정규화한다.
5. weight decay(가중치 감소)
신경망 학습의 목적은 손실 함수의 값을 줄이는 것이다. 예를 들어, 가중치의 제곱 노름(L2 노름)을 손실 함수에 더한다. 그러면 가중치가 커지는 것을 억제할 수 있다. 가중치를 W라 하면 L2노름에 따른 가중치 감소는 $\frac{1}{2} \lambda W^2$ 이 되고, $\frac{1}{2} \lambda W^2$ 을 손실 함수에 더한다. 여기에서 $\lambda$ 는 정규화의 세기를 조절하는 하이퍼파라미터이다. $\lambda& 를 크게 설정할수록 큰 가중치에 대한 페널티가 커진다.
L2노름, L1노름 등이 있는데 L2노름이 보편적이다.
6. train, evaluation, validation
- 훈련 데이터(train) : 매개변수 학습
- 검증 데이터(eval) : 하이퍼파라미터 성능 평가
- 시험 데이터(val) : 신경망의 범용 성능 평가
하이퍼 파라미터의 성능을 평가할 때는 시험 데이터를 사용해서는 안 된다. 시험 데이터를 사용하여 하이퍼 파라미터를 조정하면 하이퍼 파라미터 값이 시험 데이터에 오버피팅되기 때문이다. 즉, 하이퍼 파라미터 값의 ‘좋음’을 시험 데이터로 확인하게 되므로 하이퍼 파라미터의 값이 시험 데이터에만 적합하도록 조정되어 버린다. 그래서 하이퍼 파라미터를 조정할 때는 하이퍼 파라미터 전용 확인 데이터가 필요하다. 이를 검증 데이터라고 부른다.